自由度とは、未知の母数の値を推定して推定値の変動性を計算するために「費やす」ことが可能なデータの情報量のことです。この値は、サンプルに含まれる観測値とパラメータの数によって決定されます。
サンプルサイズを大きくすると、母集団に関して提供される情報が増え、結果的にデータの自由度が大きくなります。パラメータをモデルに追加すると(たとえば、回帰式の項数を増やす)、データから得た情報を「費やし」、パラメータ推定値の変動性の推定に利用できる自由度が下がります。
自由度は特定の分布の特徴を把握するためにも使用されます。多くの分布族(t分布、F分布、カイ二乗分布など)では、自由度を使用して、さまざまなサンプルサイズやモデルパラメータ数についてそれに適したt分布、F分布、またはカイ二乗分布を指定します。たとえば、次の図では自由度が異なるカイ二乗分布の違いを示しています。
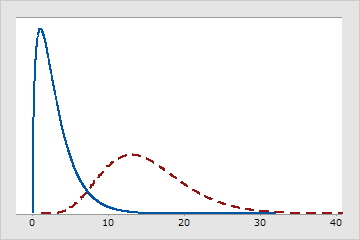
さまざまな自由度のカイ二乗分布
実線の分布は自由度が3です。点線の分布は自由度が15です。
例
たとえば、1サンプルt検定では、1つのパラメータ(母平均)のみの推定値が得られます。サンプルサイズがnの場合は、母平均とその変動性の推定に利用する情報はn個となります。自由度の1つは平均の推定に費やされ、残りの(n-1)個の自由度で変動性が推定されます。そのため、1サンプルt検定では(n-1)個の自由度があるt分布を使用します。
反対に、重回帰ではモデルに含める各項のパラメータを推定する必要があり、それぞれで自由度を消費します。そのため、重回帰モデルの項を多くしすぎると、パラメータの変動性の推定に利用できる自由度が減り、信頼性が低くなります。
