正規分布とは、平均からの一連の標準偏差によってデータ観測値の割合を推定するベンチマークが確立されるつりがね型の分布です。これらのベンチマークに基づいて、Z検定やt検定などの多くの仮説検定が行われます。
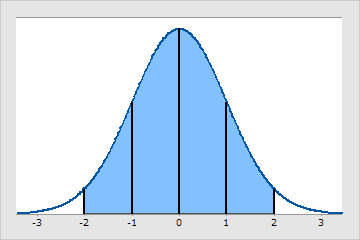
仮説正規分布のヒストグラム
このデータの分布は正規分布であるため、値の何パーセントが特定の範囲に含まれるかを正確に知ることができます。次に例を示します。
- 観測値の約95%は平均の2サンプルの標準偏差以内にあります(青い影の付いた領域)。値の95%が、平均の標準偏差の1.96(−1.96と+1.96の間)に含まれます。したがって、この範囲外にある観測値は5%(0.05)未満です。この範囲に基づいて、多くの仮説検定で0.05のα水準が採用されます。
- 観測値の68%は平均から1標準偏差以内(-1~+1)にあり、観測値の99.7%は平均から3標準偏差以内(-3~+3)にあります。
正規分布の例
ペンシルバニア州に居住するすべての成人男子の身長は、正規分布におおよそ従っています。したがって、大半の男性の身長が平均身長である69インチに近いといえます。69インチよりも身長が若干高い男性と若干低い男性の人数はほぼ同じです。身長が非常に高い男性や非常に低い男性はわずかです。この標準偏差は2.5インチです。
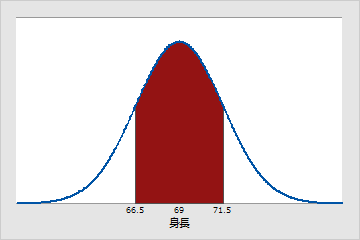
おおよそ68%のペンシルバニア州の成人男子の身長が、66.5(μ - 1σ)インチから71.5(μ + 1σ)インチとなります。
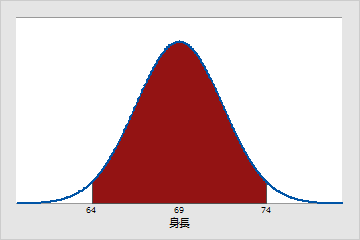
おおよそ95%のペンシルバニア州の成人男子の身長が、64(μ - 2σ)インチから74(μ + 2σ)インチとなります。
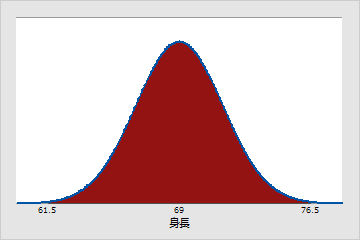
おおよそ99.7%のペンシルバニア州の成人男子の身長が、61.5(μ - 3σ)インチから76.5(μ + 3σ)インチとなります。
