アンダーソンｰダーリング（Anderson-Darling）統計量

Anderson-Darling統計量は、データが特定の分布にどの程度適合するかを測定します。特定のデータセットおよび分布に対して、分布がデータに適合するほど、この統計量は小さくなります。たとえば、Anderson-Darling統計量を使用して、データがt検定の正規性の仮定を満たすかどうかを判断できます。

対応するp値（ある場合）を使用して、データが選択した分布からのものかどうかを検定します。p値が選択したα水準（通常は0.05または0.10）未満の場合は、データがその分布からのものであるという帰無仮説を棄却します。Minitabでは、Anderson-Darling検定のp値が表示されないことがあります。

Anderson-Darling統計量を使用して、複数の分布の適合度を比較してどの分布が最適かを判断できます。ただし、1つの分布が最適であると結論付けるためには、そのAnderson-Darling統計量が他よりもかなり低い必要があります。統計量が互いに近い場合、確率プロットなどの追加の基準を使用して最適な分布を選択する必要があります。

分布	Anderson-Darling	p値
指数	9.599	p < 0.003
正規	0.641	p < 0.089
3パラメータワイブル	0.376	p < 0.432

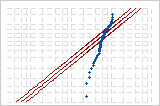
指数

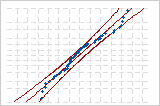
正規

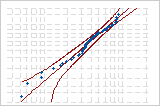
3パラメータワイブル

Minitabでは、（選択した分布に基づき、最尤推定法または最小二乗推定のいずれかを使用する）確率プロットの適合線とノンパラメトリックステップ関数の間の二乗距離に重みを付けたものを使用してAnderson-Darling統計量が計算されます。この計算では、分布の裾に近づくにつれて重みが大きくなっています。