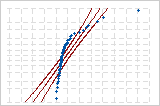
確率プロットでは、正式ではありませんが、おおよその判断を下す「太鉛筆検定」という正規性検定がよく使用されます。「太鉛筆」が適合線上に置かれているのを想像してみましょう。
- プロット上のすべてのデータ点が含まれる場合、データはおおよそ正規です。
- 点が適合線から遠く離れていて、太鉛筆の端から見えるようであれば、データはおおよそ非正規です。
この非公式な方法は、正規性検定そのものから得られる統計的な推測の代わりとはなりませんが、すばやく視覚的判断を下すのには便利です。太鉛筆検定は次の確率プロットに適用されます。帯は適合線上に置かれた太鉛筆を表しています。
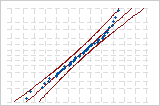
正規データでの「太鉛筆検定」