特定の母集団特性(平均など)に関する情報を判断する場合、母集団全体は測定することができないため、通常は母集団からランダムサンプルを抽出します。そのサンプルを使用して対応するサンプル特性を計算し、そのサンプル特性を不明な母集団特性についての情報の要約に使用します。この対象となる母集団特性はパラメータと呼ばれ、対応するサンプル特性はサンプル統計量またはパラメータ推定値と呼ばれます。統計量はサンプルから取得したパラメータについての情報の要約であるため、統計量の値は母集団から抽出された特定のサンプルによって異なります。その値は各ランダムサンプル間でランダムに変化するため、統計量はランダム量(変数)です。このランダム変数の確率分布はサンプル分布と呼ばれます。(サンプル)統計量のサンプル分布は、ランダムサンプルに基づいて対応する母集団パラメータについての結論を導くことができるため、重要です。
たとえば、正規分布の母集団からランダムサンプルを抽出する場合、そのサンプル平均が統計量です。抽出したサンプルに基づくサンプル平均値は、母平均の推定値です。この推定値は、同じ正規母集団から別のサンプルが抽出された場合はランダムに変化します。この変化を表す確率分布は、サンプル平均のサンプル分布です。統計量のサンプル分布では、考えられるすべての統計値、および統計量の値の範囲が発生する頻度が示されます。親母集団が正規である場合、サンプル平均のサンプル分布も正規になります。
以下のセクションで、パラメータ、パラメータ推定値、およびサンプル分布について詳細に説明します。
パラメータについて
パラメータとは、分布曲線を生成するために確率分布関数(PDF)の入力に使用できる母集団全体の記述的測度です。サンプルの統計量と区別するため、パラメータは通常ギリシャ文字で示されます。たとえば、母平均はギリシャ文字のミュー(μ)で表され、母集団の標準偏差はギリシャ文字のシグマ(σ)で表されます。パラメータは固定定数です。つまり、変数のように変化しません。ただし、母集団全体を測定することができないため、通常その値は不明です。
| 分布 | パラメータ1 | パラメータ2 | パラメータ3 |
|---|---|---|---|
| カイ二乗 | 自由度 | ||
| 正規 | 平均 | 標準偏差 | |
| 3パラメータガンマ | 形状 | スケール | しきい値 |
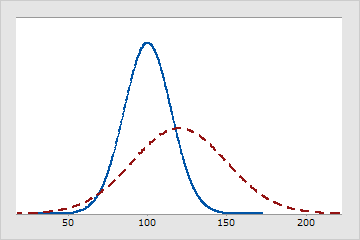
実線は、平均が100で標準偏差が15の正規分布を表します。点線も正規分布ですが、平均は120で標準偏差は30です。
パラメータ推定値(サンプル統計量)について
パラメータとは、母集団全体の記述的測度です。ただし、母集団全体を測定することができないため、通常その値は不明です。したがって、母集団からランダムサンプルを抽出してパラメータ推定値を取得できます。統計分析の目的の1つは、母集団パラメータの推定値と、これらの推定値に付随する誤差の量を得ることです。これらの推定値は、サンプル統計量とも呼ばれています。
- 点推定値は、パラメータの最も可能性がある単一の値です。たとえば、母平均(パラメータ)の点推定値はサンプルの平均値(パラメータ推定値)です。
- 信頼区間とは、母集団パラメータの含まれる可能性が高い値の範囲です。
たとえば、スパークプラグのメーカーで自社のプラグギャップの問題について調べているとします。作成したすべてのスパークプラグを1つずつ測定するには費用がかかりすぎます。そこで、ランダムに100個のスパークプラグを選び出し、ギャップをミリメートル単位で測定することにします。サンプルの平均は9.2でした。これが母平均の点推定値(μ)です。また、μに対して95%の信頼区間を設定すると、(8.8, 9.6)となります。つまり、すべてのスパークプラグギャップの真の平均値が8.8~9.6の間になる信頼度は95%になります。
サンプル分布について
| カボチャ | 1 | 2 | 3 | 4 | 5 | 6 |
| 重量 | 19 | 14 | 15 | 12 | 16 | 17 |
母集団全体がわかっていますが、説明用として3個のカボチャを含む母集団で考えられるすべてのランダムサンプル(20ランダムサンプル)を抽出します。次に、各サンプルの平均を計算します。サンプル平均のサンプル分布は、3個のカボチャで考えられるすべてのランダムサンプルのすべてのサンプル平均で表され、次の表にこれが示されています。
| サンプル | 重量 | 平均重量 | 確率 |
|---|---|---|---|
| 2、3、4 | 14、15、12 | 13.7 | 1/20 |
| 2、4、5 | 14、12、16 | 14 | 1/20 |
| 2、4、6 | 14、12、17 | 14.3 | 2/20 |
| 3、4、5 | 15、12、16 | ||
| 3、4、6 | 15、12、17 | 14.7 | 1/20 |
| 1、2、4 | 19、14、12 | 15 | 3/20 |
| 2、3、5 | 14、15、16 | ||
| 4、5、6 | 12、16、17 | ||
| 2、3、6 | 14、15、17 | 15.3 | 2/20 |
| 1、3、4 | 19、15、12 | ||
| 1、4、5 | 19、12、16 | 15.7 | 2/20 |
| 2、5、6 | 14、16、17 | ||
| 1、2、3 | 19、14、15 | 16 | 3/20 |
| 3、5、6 | 15、16、17 | ||
| 1、4、6 | 19、12、17 | ||
| 1、2、5 | 19、14、16 | 16.3 | 1/20 |
| 1、2、6 | 19、14、17 | 16.7 | 2/20 |
| 1、3、5 | 19、15、16 | ||
| 1、3、6 | 19、15、17 | 17 | 1/20 |
| 1、5、6 | 19、16、17 | 17.3 | 1/20 |
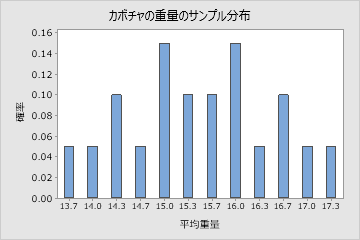
実際には、上記の説明例のようなサンプル分布を表にすることはできません。サンプルの親母集団がわかっている最良のシナリオでも、対象となるサンプル統計量の正確なサンプル分布は判断できません。ただし、場合によってはサンプル統計量のサンプル分布を近似できる可能性があります。たとえば、正規母集団からサンプルを抽出した場合、サンプル平均は完全な正規分布になります。
正規母集団以外の母集団からサンプルを抽出すると、サンプル平均の正確な分布は判断できない可能性があります。ただし、中心極限定理により、サンプルが十分に大きい場合はサンプル平均がほぼ正規に分布されます。母集団が不明でサンプルが十分に大きい場合は、たとえば、サンプル平均が母平均のある特定の数の標準偏差内に収まる確実度は約85%であると言うことができます。
