このトピックの内容
相関とは
相関係数は、2変数が連動して変化する傾向の度合いを測定します。係数は、関係の強度と方向の両方を示します。Minitabには、2つの異なる相関分析があります。
- ピアソンの積率相関
-
ピアソンの相関は、2つの連続変数間の線形関係を評価します。一方の変数が変化したときにもう一方の変数が比例して変化する場合、関係は線形です。
たとえば、ピアソン相関を使用して、製造施設の温度上昇がチョコレートコーティングの厚さの減少に関係しているかを調べる場合があります。
- スピアマンの順位相関
-
スピアマンの相関は、2つの連続変数または順位変数間の単調関係を評価します。単調関係では変数が一緒に変化しますが、一定の割合とは限りません。スピアマンの相関係数は、生データではなく各変数の順位値に基づきます。
スピアマンの相関は、順位変数を含む関係を評価するためによく使用されます。たとえば、スピアマンの相関を使用して、従業員が試験を完了する順序が雇用期間と関連しているかどうかを評価する場合があります。
散布図を使用して変数間の関係を調べるのは常に良い考えです。相関係数は、線形(ピアソン)または単調(スピアマン)関係のみを測定します。その他の関係も考えられます。
ピアソンの係数とスピアマンの係数の比較
ピアソンの相関係数とスピアマンの相関係数は、−1~+1の値の範囲で変化します。ピアソンの相関係数が+1の場合、一方の変数が増加すると、もう一方の変数が一定量増加します。この関係は完全に直線になります。この場合、スピアマンの相関係数も+1になります。


ピアソン = +1、スピアマン = +1
一方の変数が増加したときにもう一方の変数が増加するという関係であっても、その量が一定でない場合、ピアソンの相関係数は正ですが+1より小さくなります。この場合、スピアマンの係数はまだ+1のままです。

ピアソン = +0.851、スピアマン = +1
関係がランダムまたは存在しない場合、両方の相関係数がほぼ0になります。


ピアソン = −0.093、スピアマン = −0.093
減少関係で関係が完全に線形の場合、両方の相関係数が−1になります。


ピアソン = −1、スピアマン = −1
一方の変数が減少したときにもう一方の変数が増加するという関係であっても、その量が一定でない場合、ピアソンの相関係数は負ですが−1より大きくなります。この場合、スピアマンの係数はまだ−1のままです。


ピアソン = −0.799、スピアマン = −1
相関値が−1または1の場合、円の半径と外周に見られるような完全な線形関係を示します。しかし、相関値の真の価値は、完全ではない関係を数量化することにあります。2つの変数が相関していることが検出されると、回帰分析によって関係の詳細が示されます。
その他の線形関係
ピアソンの相関係数は、線形関係のみを測定します。スピアマンの相関係数は、単調関係のみを測定します。そのため、相関係数が0であったとしても意味のある関係が存在している可能性があります。関係があるかどうかを判断するには、散布図を調べます。
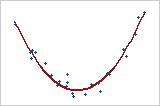

係数が0の場合
このグラフは、非常に強い関係を示しています。ピアソンの係数とスピアマンの係数はどちらもほぼ0です。
