棄却値とは、帰無仮説での検定統計量の分布で帰無仮説を棄却するために必要な値のセットを定義する点です。このセットは、棄却域と呼ばれます。通常、片側検定には1つの棄却値があり、両側検定には2つの棄却値があります。棄却値は、帰無仮説の場合に検定統計量が検定の棄却域に1つの値を持つ確率が有意水準（αまたはアルファで示される）と完全に等しくなるように決定されます。
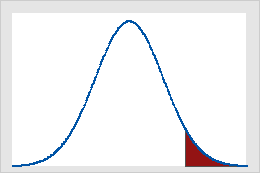
図A
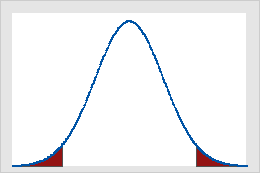
図B
標準正規分布の棄却値は、α = 0.05となります。
図Aは、検定統計量がこの場合の棄却値である1.64以上の場合、片裾Z検定の結果が有意であることを示しています。影の付いた部分は、曲線の下の部分の第1種の過誤（この例ではα = 5%）の確率を表しています。図Bは、検定統計量の絶対値がこの場合の棄却値である1.96以上の場合、両裾Z検定の結果が有意であることを示しています。2つの影の付いた部分の合計は曲線の下の部分の5%（α）を占めます。
棄却値の計算例
仮説検定では、H0を棄却するかH0を棄却しないのに十分な証拠がサンプルにあるかどうかを判断する方法が2つあります。最も一般的な方法は、p値を事前に指定したαの値と比較する方法です。ここで、αはH0が真である場合にH0を棄却する確率です。さらに、データに基づいた検定統計量の計算値を棄却値と比較することもできます。次は、1サンプルt検定と一元配置分散分析（ANOVA）の棄却値を計算する方法の例です。
1サンプルt検定の棄却値の計算
10個の観測値で1サンプルt検定を実行していて、両裾の対立仮説（つまり、H1が等しくない）があり、0.10というαを使用するとします。
- を選択します。
- 逆累積確率を選択します。
- 自由度に9（観測値の数から1を引いたもの）を入力します。
- 定数で入力に0.95（1からαの半分を引いたもの）を入力します。
これにより、逆累積確率が得られ、棄却値である1.83311と等しくなります。t統計量の値の絶対値がこの棄却値より大きい場合、有意水準0.10において帰無仮説H0を棄却できます。
分散分析（ANOVA）の棄却値の計算
12個の観測値で一元配置分散分析を実行していて、因子に水準が3つあり、0.05というαを使用するとします。
- を選択します。
- 逆累積確率を選択します。
- 分子自由度に2（因子水準の数から1を引いたもの）を入力します。
- 分母の自由度に9（誤差の自由度）を入力します。
- 定数で入力に0.95（1からαを引いたもの）を入力します。
これにより、逆累積確率（棄却値）が4.25649と求められます。F統計量がこの棄却値より大きい場合、有意水準0.05において帰無仮説H0を棄却できます。
