信頼区間とは、未知の母数の値を含むと考えられる値の範囲で、サンプル統計量から得られます。ランダムな性質上、同じ母集団からの2つのサンプルにおいて同一の信頼区間が得られるという可能性は低いと言えます。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間の特定の割合に未知の母数が含まれることになります。
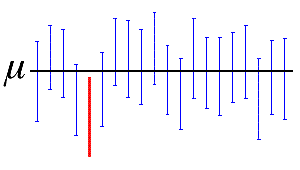
ここでは、黒の水平線は不明な母平均µの固定値を表します。水平線に重なる青の垂直信頼区間には、母平均の値が含まれます。水平線とは重ならず下にある赤の信頼区間にはこの値は含まれません。95%の信頼区間は、同じ母集団から抽出した20個のサンプルのうち19個(95%)で母数を含む信頼区間を得られることを示しています。
信頼区間を使用すると、母数の推定値を評価できます。たとえば、製造会社が、生産する鉛筆の平均の長さが目標の長さと異なるかどうかを調べるとします。鉛筆のランダムサンプルを抽出し、サンプルの平均の長さは52ミリで95%信頼区間が(50,54)であることがわかりました。したがって、95%の信頼度ですべての鉛筆の平均の長さが50~54ミリであると言えます。
- 点推定
- この単一値は、サンプルデータを使用して母数を推定するためのものです。
- 誤差幅
-
統計量を使用して値を推定する場合、どれほど入念に分析を計画しても、推定値はランダムなサンプリング誤差の影響を受けることに注意してください。誤差幅はこの誤差を数量化し、推定値の精度を示します。
誤差幅は調査結果に関連しているため、誤差幅については一般的に知られていると思われます。たとえば、政党の世論調査で、誤差幅5%で候補者の支持率が55%だと報告されることがあります。これは、実際の支持率は+/- 5%であり、50%から60%の間であることを意味します。
両側信頼区間の場合、誤差幅は、推定統計量から信頼区間の各値までの距離です。信頼区間が対称的な場合、誤差幅は信頼区間の幅の半分です。たとえば、カム軸の平均推定長さは600ミリで、信頼区間範囲は599~601です。誤差幅は1です。
誤差幅が大きいほど区間は広くなり、点推定値の信頼度が低くなります。
