2変数間の関係を評価する場合、変数がどのような関係になっているかを判断することが重要です。線形関係は最も一般的ですが、変数は下で示しているように、非線形または単調関係になる場合もあります。変数間に関係が存在しない場合もあります。関係を評価するには、まず変数の散布図を作成する必要があります。
線形関係は、直線でモデル化されるデータの傾向です。たとえば、ある航空会社が飛行コストに対する燃料価格の影響を推定します。ジェット燃料が1ガロンにつき1ドル増加すると、ロサンゼルスとニューヨークの間の飛行コストが約3500ドル値上がりすることがわかりました。これは、ジェット燃料の費用と飛行コストの間に線形関係があることを表しています。
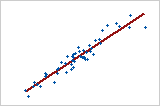
プロット1: 強い正の線形関係
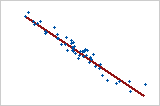
プロット2: 強い負の線形関係
双方の変数が同時に一定の割合で増加または減少する場合には、正の線形関係が存在します。プロット1のデータ点は直線付近に位置しており、変数間の関係が強いことを示しています。この関係のピアソン相関係数は+0.921です。
1つの変数が増加したとき他方の変数が減少する場合には、負の線形関係が存在します。プロット2のデータ点は直線付近に位置しており、変数間の関係が強いことを示しています。この関係のピアソン相関係数は−0.968です。
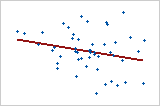
プロット3: 弱い線形関係
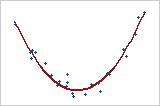
プロット4: 非線形関係
プロット3のデータ点は、ランダムに分布しているように見えます。これらのデータ点は直線付近には位置しておらず、何らかの関係が存在するとしても非常に弱いものであることを示しています。この関係のピアソン相関係数は−0.253です。
2つの変数の関係が線形でない場合は、1つの変数が変わるたびに増加率または減少率も変わり、データに「曲線パターン」を生じさせます。曲線傾向がある場合は、2次関数や3次関数などの非線形関数を使ってモデル化するか、線形データに変換する方が適していることがあります。プロット4は、2変数間の強い関係を示しています。ただし、この関係は線形ではないため、ピアソン相関係数はわずか+0.244です。この関係は、存在しうる関係を調べるためにデータをプロットすることが重要である理由を示しています。
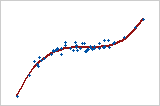
プロット5: 単調関係
単調関係では変数が同じ相対方向に移動する傾向がありますが、一定の割合とは限りません。線形関係では変数が同じ方向に一定の割合で移動します。プロット5は、両方の変数が共に増大するが同じ率で増大しているわけではないことを示しています。この関係は単調ですが、線形ではありません。これらのデータのピアソン相関係数は0.843ですが、スピアマン相関の方が高く0.948です。
線形関係も単調です。たとえば、プロット1で示している関係は単調であり線形です。
