Dixonの検定統計量
- iは、外れ値の疑いがあるデータの同じ側(低いまたは高い)にある極端な値を示します。i = 1または2です。
- jはデータの反対側にある極端な値の数を示します。j = 0、1、または2です。
たとえば、外れ値の疑いがある値がサンプルの最小値でありながら、異常に大きな値も2つサンプルに含まれている場合、r12が適切な検定統計量です。検定統計量r10(DixonのQとも呼ばれる)は、サンプルに極端な値が1つしか含まれない場合に適しています。
Dixonの検定統計量の棄却値は、Rorabacherが表にしています(1991年)。
片側検定統計量


両側検定統計量

表記
| 用語 | 説明 |
|---|---|
| rij | Dixonの検定統計量(i = 1, 2、j = 0, 1, 2) |
| yi | サンプルに含まれるi番目に小さい値 |
| n | サンプルに含まれる観測値数 |
参考文献
- D.B. Rorabacher (1991). "Statistical Treatment for Rejection of Deviant Values: Critical Values of Dixon Q Parameter and Related Subrange Ratios at the 95 percent Confidence Level," Analytic Chemistry, 83, 2, 139-146.
- E.P. King (1953). "On Some Procedures for the Rejection of Suspected Data," Journal of the American Statistical Association, Vol. 48, No. 263, 531-533.
Grubbsの検定統計量
片側統計量の計算式

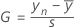
両側統計量の計算式
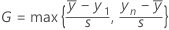
表記
| 用語 | 説明 |
|---|---|
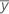 | サンプル平均 |
| yi | サンプルに含まれるi番目に小さい値 |
| s | サンプルの標準偏差 |
| n | サンプルに含まれる観測値数 |
Dixonの検定統計量のp値

検定統計量の累積分布関数
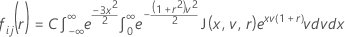

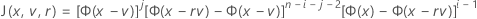
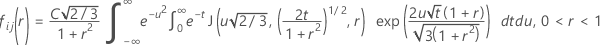
Minitabは30点のGauss-Laguerreの求積法を使用して内積分を評価します。Minitabは30点のGauss-Hermiteの求積法を使用して外積分を評価します。
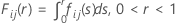
McBane(2006年)と同じように、Minitabは16点のGauss-Legendreの求積法を使用してFij(r)を計算します。
片側検定のp値

片側検定のp値

さらに、Kingは上記の近似が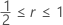 と同等になるとも述べています。
と同等になるとも述べています。
表記
| 用語 | 説明 |
|---|---|
| rij | Dixonの検定統計量(i = 1, 2、j = 0, 1, 2) |
| yi | サンプルに含まれるi番目に小さい値 |
| n | サンプルに含まれる観測値数 |
参考文献
W.J. Dixon (1951). "Ratios Involving Extreme Values," Annals of Mathematical Statistics, 22(1), 68-78.
E.P. King (1953). "On Some Procedures for the Rejection of Suspected Data," Journal of the American Statistical Association, Vol. 48, No. 263, pages 531-533.
G.C. McBane (2006). "Programs to Compute Distribution Functions and Critical Values for Extreme Value Ratios for Outlier Detection," Journal of Statistical Software, Vol. 16, No. 3, pages 1-9.
Grubbsの検定統計量のp値
片側検定の計算式

両側検定の計算式

p値は正確か近似か

満たさない場合、計算されるp値は正確なp値の上限を示します。ただし、上限は正確なp値の非常に優れた近似です。
表記
| 用語 | 説明 |
|---|---|
| G | Grubbsの検定統計量 |
| n | サンプルに含まれる観測値数 |
| T | 自由度がn – 2のt分布として分布するランダム変数 |
