目的の方法または計算式を選択してください。
平均
一連の数字の中心として一般的に使用される測度。平均は平均値とも呼ばれます。これは、すべての観測値の和を（非欠損）観測値数で割ったものです。
計算式
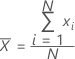
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の観測値 |
| N | 非欠損観測値の数 |
標準偏差
サンプルの標準偏差により、データの広がりの測度が得られます。サンプル分散の平方根に等しくなります。
計算式
列にx 1, x 2,..., x Nが含まれていて、平均が
の場合、サンプルの標準偏差は次のようになります。
の場合、サンプルの標準偏差は次のようになります。
表記
| 用語 | 説明 |
|---|---|
| x i | i番目の観測値 |
 | 観測値の平均 |
| N | 非欠損観測値の数 |
N
Minitabは、サンプルに含まれる非欠損観測値の数を表示します。
Anderson-Darling統計量 (A2)
A2は、（選択分布に基づいた）適合線と（プロット点に基づいた）ノンパラメトリックステップ関数の間のエリアを示します。この統計量は、分布の裾の方が重みの大きい二乗距離です。Anderson-Darlingの値が小さい場合、分布がデータにより良くあてはまることを示します。
Anderson-Darling正規性検定は次のように定義されます。
H0: データは正規分布に従う
H1: データは正規分布に従わない
計算式
表記
| 用語 | 説明 |
|---|---|
| F(Yi) |  、これは標準正規分布の累積分布関数です |
| Yi | 順序付きデータ |
ライアン・ジョイナー(R)
ライアン・ジョイナー検定では、データとデータの正規スコアの間の相関を示す相関係数が得られます。相関係数が1に近い場合、データは正規確率プロットに近くなります。適切な棄却限界値より小さい場合、正規性の帰無仮説を棄却します。
計算式
相関係数は、次のように計算されます。
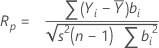
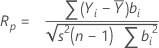
表記
| 用語 | 説明 |
|---|---|
| Yi | 順序付けされた観測値 |
| bi | 順位付けされたデータの正規スコア |
| s2 | サンプル分散 |
Kolmogorov-Smirnov
計算式
Kolmogorov-Smirnov検定は次のように定義されます。
- H0: データは正規分布に従う
- H1: データは正規分布に従わない
Kolmogorov-Smirnov検定統計量は次のように定義されます。
表記
| 用語 | 説明 |
|---|---|
| D+ | maxi {i / n – Z (i)} |
| D– | maxi {Z (i) – (i – 1) / n)} |
| Z | F(X(i)) |
| F(x) | 正規分布の確率分布関数 |
| X(i) | ランダムサンプルのi番目の順序統計量（1 ≤ i ≤ n） |
| n | サンプルサイズ |
p値
正規性検定の結果をレポートするためのもう1つの定量的な測度はp値です。p値が小さい場合、帰無仮説が誤っていることを示します。
A2がわかっている場合、p値を計算できます。次のように定義します。
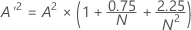
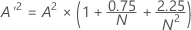
A'2に応じて、次の計算式でpを計算します。
- 13 > A'2 > 0.600の場合、p = exp(1.2937 - 5.709 * A'2 + 0.0186(A'2)2)
- 0.600 > A'2 > 0.340の場合、p = exp(0.9177 - 4.279 * A'2 – 1.38(A'2)2)
- 0.340 > A'2 > 0.200の場合、p = 1 – exp(–8.318 + 42.796 * A'2 – 59.938(A'2)2)
- A'2 <0.200の場合、p = 1 – exp(–13.436 + 101.14 * A'2 – 223.73(A'2)2)
プロット点
一般に、点の位置が適合線に近ければ、適合度が高いといえます。Minitabでは、2つの適合度の測度を利用して、データへの分布の適合度を評価することができます。
計算式
下の表は、中心線がどのように決まるかを示しています。
| 分布 | x座標 | y座標 |
|---|---|---|
| 正規 | x | Φ–1 norm |
表記
| 用語 | 説明 |
|---|---|
| Φ–1 norm | 標準正規分布の逆累積分布関数によってpに返される値 |
確率プロット
入力データはx値としてプロットされます。Minitabは、分布を仮定せずに出現の確率を計算します。グラフのYスケールは、データが正規分布になっていると、確率プロットが直線になる正規確率紙のYスケールに似ています。
