平均
平均は、データの中心を表す1つの値でサンプルを記述します。平均はデータの平均値として計算され、すべての観測値の和を観測値の数で割ったものです。
N
サンプルサイズ(N)とは、サンプルに含まれる観測値の総数です。
解釈
サンプルサイズは、検定の検出力に影響を与えます。
通常、サンプルサイズが大きくなると、検定でサンプルデータと正規分布の差を検出する検出力がより強くなります。つまり、差が実際に存在する場合、サンプルサイズが大きい方が検出できる可能性が高くなります。
標準偏差
標準偏差とは、散布度、つまり平均からのデータの広がり方を表す最も一般的な測度です。サンプルの標準偏差が大きい場合、データが平均からより広がっていることを示します。
AD
Anderson-Darlingの適合度統計量(AD)は、(正規分布に基づいた)適合線と(データ点に基づいた)経験的分布関数の間のエリアを測定します。Anderson-Darling統計量は、分布の裾の方が重みの大きい二乗距離です。
解釈
Minitabは、Anderson-Darling統計量を使用してp値を計算します。p値は帰無仮説を棄却するための証拠を測定する確率です。p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。Anderson-Darling統計量の値が大きい場合、データが正規分布に従わないことを示します。
KS
Kolmogorov-Smirnov検定では、サンプルデータのECDF(経験的累積分布関数)が、データが正規だった場合に期待される分布と比較されます。
解釈
Minitabは、Kolmogorov-Smirnov統計量を使用してp値を計算します。p値とは、データが正規である場合に、少なくともサンプルから計算される値と同じだけ極端な値として検定統計量(Kolmogorov-Smirnov統計量など)が得られる確率です。Kolmogorov-Smirnov統計量の値が大きい場合、データが正規分布に従わないことを示します。
RJ
Ryan-Joiner統計量は、データとデータの正規スコアの間の相関を計算することで、データがどれだけ正規分布に従うかを測定します。相関係数が1に近い場合は、母集団が正規である可能性が高いといえます。この検定は、Shapiro-Wilkの検定に類似しています。
解釈
Minitabは、Ryan-Joiner統計量を使用してp値を計算します。p値とは、データが正規である場合に、少なくともサンプルから計算される値と同じだけ極端な値として検定統計量(Ryan-Joiner統計量など)が得られる確率です。Ryan-Joiner統計量の値が大きい場合、データが正規分布に従わないことを示します。
p値
p値は帰無仮説を棄却するための証拠を測定する確率です。p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。
解釈
p値を使用して、データが正規分布に従わないかどうかを判断します。
- p値 ≤ α: データは正規分布に従いません(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下し、データは正規分布に従わないと結論付けます。
- p値 > α: データは正規分布に従わないと結論付けることはできません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。データは正規分布に従わないと結論付けるだけの十分な証拠はありません。
確率プロット
確率プロットは、各観測値の値を観測値の推定累積確率に対比させてプロットすることにより、サンプルから推定累積分布関数(CDF)を作成します。
解釈
確率プロットを使用して、正規分布に対するデータの適合度を視覚化します。
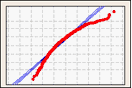
右方向に歪んだデータ
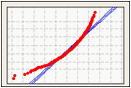
左方向に歪んだデータ
ヒント
Minitabでは、適合分布線の上にポインタを置くと、百分位数と値の図が表示されます。
