ポアソンの適合度検定を解釈するには、次の手順を実行します。主要な結果には、p値、および複数のグラフが含まれます。
ステップ1: データがポアソン分布に従わないかどうかを判定する
データがポアソン分布に従わないかどうかを判断するには、p値を有意水準(α)と比較します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準が0.05の場合は、データが確かにポアソン分布に従うときに、そのデータはポアソン分布に従わないと結論付けるリスクが5%あることを示します。
- p値 ≤ α: データはポアソン分布に従いません(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下し、データはポアソン分布に従わないと結論付けます。
- p値 > α: データはポアソン分布に従わないと結論付けることはできません(H0を棄却しない)
- p値が有意水準より大きい場合は、データはポアソン分布に従わないと結論付けるだけの十分な証拠がないため、帰無仮説を棄却しない決定を下します。
方法
| 観測値の度数 |
|---|
記述統計量
| N | 平均 |
|---|---|
| 300 | 0.536667 |
欠陥数に対する観測度数と期待度数
| 欠陥数 | ポアソン確率分布 | 観測度数 | 期待度数 | カイ二乗への寄与度 |
|---|---|---|---|---|
| 0 | 0.584694 | 213 | 175.408 | 8.056 |
| 1 | 0.313786 | 41 | 94.136 | 29.993 |
| 2 | 0.084199 | 18 | 25.260 | 2.086 |
| >=3 | 0.017321 | 28 | 5.196 | 100.072 |
カイ二乗検定
| 帰無仮説 | H₀: データはポアソン分布に従っている |
|---|---|
| 対立仮説 | H₁: データはポアソン分布に従っていない |
| 自由度 | カイ二乗 | p値 |
|---|---|---|
| 2 | 140.208 | 0.000 |
主要な結果: p値
この結果で、帰無仮説では、データがポアソン分布に従うと仮定します。p値が0.000で有意水準0.05より小さいため、帰無仮説を棄却します。データがポアソン分布から採取したものではないと結論付けることができます。
ステップ2: 各カテゴリの観測値と期待値の差を調べる
観測値と期待値の棒グラフを使用して、各カテゴリで観測値数が期待値数と異なるかどうかを判断します。観測値と期待値の差が大きい場合は、データがポアソン分布に従っていないことを意味します。
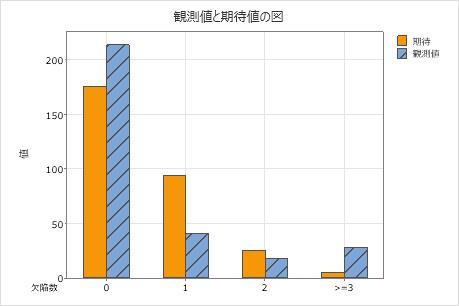
この棒グラフは、欠陥数が0、1、および3を超える場合の観測値が期待値と異なることを示してします。したがって、データがポアソン分布に従っていないとp値が示していることを棒グラフで視覚的に確認できます。
