ある家電会社の品質エンジニアが、テレビ1台当たりの欠陥数がポワソン分布に従っているかどうかを知りたいと考えています。エンジニアは、300台のテレビを無作為に抽出し、テレビ1台当たりの欠陥数を記録します。
- サンプルデータテレビの欠陥.MWXを開きます。
- を選択します。
- 変数に欠陥数を入力します。
- 度数変数: （オプション）に観測値を入力します。
- OKをクリックします。
結果を解釈する
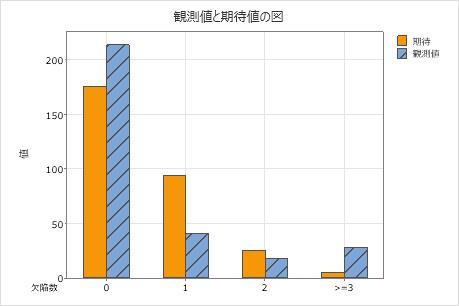
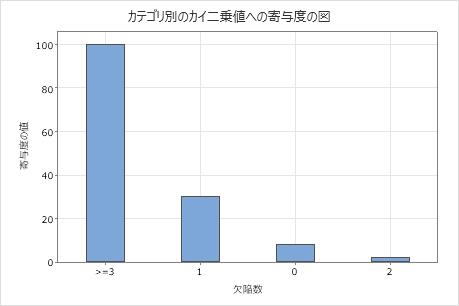
帰無仮説では、データがポアソン分布に従うと仮定します。p値が0.000で有意水準0.05より小さいため、エンジニアは帰無仮説を棄却し、データがポアソン分布に従わないと結論付けます。グラフは、観測値と期待値の差がカテゴリ1と
3で大きく、カテゴリ3のカイ二乗統計量への寄与度が最大であることを示しています。
方法
| 観測値の度数 |
|---|
記述統計量
| N | 平均 |
|---|---|
| 300 | 0.536667 |
欠陥数に対する観測度数と期待度数
| 欠陥数 | ポアソン確率分布 | 観測度数 | 期待度数 | カイ二乗への寄与度 |
|---|---|---|---|---|
| 0 | 0.584694 | 213 | 175.408 | 8.056 |
| 1 | 0.313786 | 41 | 94.136 | 29.993 |
| 2 | 0.084199 | 18 | 25.260 | 2.086 |
| >=3 | 0.017321 | 28 | 5.196 | 100.072 |
カイ二乗検定
| 帰無仮説 | H₀: データはポアソン分布に従っている |
|---|---|
| 対立仮説 | H₁: データはポアソン分布に従っていない |
| 自由度 | カイ二乗 | p値 |
|---|---|---|
| 2 | 140.208 | 0.000 |
