このトピックの内容
ステップ1: サンプルのサイズを記述する
Nを使用して、サンプルに含まれる観測値の数を調べます。Minitabでは、この数に欠損値を含めていません。
中規模から大規模のデータのサンプルを収集する必要があります。少なくとも20個の観測値を持つサンプルであれば、データの分布を表すのに十分です。しかしながら、より分かりやすくヒストグラムで分布を表すには少なくとも50個の観測値が必要であると推奨する主張もあります。サンプルサイズが大きいほど、平均や標準偏差などの工程パラメータをより正確に推定できます。
統計量
| 変数 | N | 欠損値 | 平均 | 平均の標準誤差 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|---|---|---|---|
| トルク | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要な結果: N
この結果には、観測値が68個あります。
ステップ2: データの中心を記述する
データの中心を表す1つの値でサンプルを表すのに、平均を使います。多くの統計分析では、平均がデータ分布の中央の標準測度として使用されます。
中央値もまた、データ分布の中央の測度を指します。中央値は平均に比べて外れ値の影響を受けにくくなっています。データ値の半分は中央値より大きく、半分は中央値未満です。
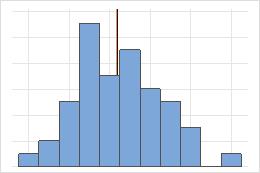
対称
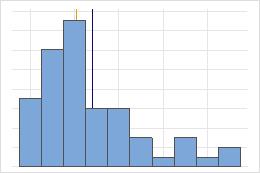
非対称
対称分布の場合、平均値(青い線)と中央値(オレンジ色の線)は非常によく似ているため、両方の線を簡単に確認することはできません。ただし、非対称分布は右側に歪んでいます。
統計量
| 変数 | N | 欠損値 | 平均 | 平均の標準誤差 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|---|---|---|---|
| トルク | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要な結果: 平均と中央値
この結果で、歯磨き粉のキャップを外すのに必要な平均トルクは21.265、トルクの中央値は20です。このデータは右に歪んでいるように見えます。そのため、平均が中央値よりも高くなっています。
ステップ3: データの広がりを記述する
標準偏差を使用して、平均からのデータの拡散程度を判断します。 標準偏差の値が高いほど、データの広がりが大きいことを示します。
統計量
| 変数 | N | 欠損値 | 平均 | 平均の標準誤差 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|---|---|---|---|
| トルク | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要な結果: 標準偏差
この結果で、標準偏差は6.422です。正規データでは、ほとんどの観測値は平均のそれぞれの側で標準偏差の3倍以内の広がりになります。
ステップ4: データ分布の形状と広がりを評価する
ヒストグラム、個別値プロット、および箱ひげ図を使用して、データの形状と広がりを評価し、潜在的な外れ値を識別します。
データの広がりを調べて、データが歪んで見えるかどうかを判断する
データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。
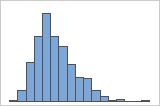
右方向の歪み
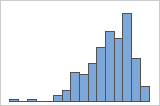
左方向の歪み
データが右方向に歪んだヒストグラムは、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだヒストグラムは、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
データにどれだけ変動性があるかを判断する
点の広がりを評価して、サンプルがどの程度変動しているかを判断します。サンプル内の変動が大きいほど、データの中心からの点の広がりが大きくなります。

この個別値プロットは、左側のデータよりも右側のデータの方が変動が大きいことを示しています。
マルチモーダルデータを探す
多峰性データには複数の頂点があり、最頻値とも呼ばれます。多くの場合、多峰性データは重要な変数がまだ説明されていないことを意味します。
観測値をグループに分類できる追加情報がある場合は、その情報でグループ変数を作成できます。その後そのグループでグラフを作成し、グループ変数でデータの頂点が説明されるかどうかを判断できます。
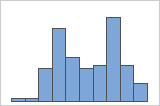
単純
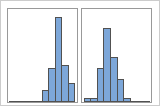
グループ
たとえば、銀行のマネージャが待ち時間データを収集し、単純ヒストグラムを作成しているとします。そのヒストグラムには2つの頂点があります。さらに調べると、小切手を換金する顧客の待ち時間は住宅担保ローンを申し込む顧客の待ち時間よりも短いことがわかりました。マネージャは顧客業務用のグループ変数を追加し、グループによるヒストグラムを作成します。
外れ値を識別する
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。
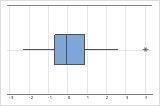
箱ひげ図では、アスタリスク(*)で外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
ステップ5: 異なるグループのデータを比較する
データ内のグループを識別する[グループ変数]がある場合、これを使用してグループ別またはグループレベル別にデータを分析できます。
統計量
| 変数 | 機械 | N | 欠損値 | 平均 | 平均の標準誤差 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| トルク | 1 | 36 | 0 | 18.6667 | 0.732467 | 4.39480 | 10 | 15.25 | 17 | 21.75 | 30 |
| 2 | 32 | 0 | 24.1875 | 1.25839 | 7.11852 | 14 | 17.5 | 24 | 31 | 37 |
この結果で、要約統計量は機械ごとに計算されます。各機械のデータの中心と広がりの違いが簡単にわかります。たとえば、機械1では機械2と比べて平均トルクが低く、変動性が低くなっています。平均の差が有意かどうかを判断するには、2サンプルt検定を実行します。
