このトピックの内容
箱ひげ図
箱ひげ図は、サンプルの分布を視覚的に要約します。データの形状、中心傾向、および変動性が表示されます。
解釈
箱ひげ図を使用して、データの広がりを調べ、潜在的な外れ値を識別します。 箱ひげ図は、サンプルサイズが20より大きい場合に最適です。
- 歪んだデータ
-
データの広がりを調べて、データが歪んでいるかどうかを判断します。データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。

右方向の歪み

左方向の歪み
データが右方向に歪んだ箱ひげ図は、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだ箱ひげ図は、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。
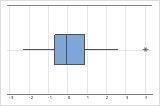
箱ひげ図では、アスタリスク(*)で外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
ヒストグラム
ヒストグラムは、サンプル値を多数の区間に分割し、各区間内のデータ値の度数をバーで表します。
解釈
ヒストグラムを使用してデータの形状と広がりを評価します。 ヒストグラムは、サンプルサイズが20より大きい場合に最適です。
- 歪んだデータ
-
正規分布曲線を重ねたヒストグラムを使用して、データが正規分布であるかどうかを調査できます。正規分布は、曲線で示されるように、左右対称でつりがね型をしています。多くの場合、サンプルサイズが小さいと正規性評価が難しくなります。確率分布プロットは、分布の適合の判断に最適です。
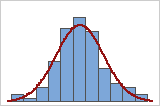
良好な適合
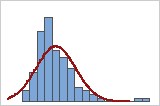
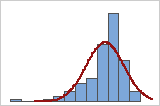
不適合
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。

ヒストグラムでは、グラフのどちらかの端にある孤立したバーで潜在的な外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
- マルチモーダルデータ
-
多峰性データには複数の頂点があり、最頻値とも呼ばれます。多くの場合、多峰性データは重要な変数がまだ説明されていないことを意味します。
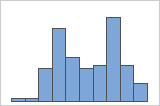
単純
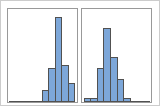
グループ
たとえば、銀行のマネージャが待ち時間データを収集し、単純ヒストグラムを作成しているとします。そのヒストグラムには2つの頂点があります。さらに調べると、小切手を換金する顧客の待ち時間は住宅担保ローンを申し込む顧客の待ち時間よりも短いことがわかりました。マネージャは顧客業務用のグループ変数を追加し、グループによるヒストグラムを作成します。
観測値をグループに分類できる追加情報がある場合は、その情報でグループ変数を作成できます。その後そのグループでグラフを作成し、グループ変数でデータの頂点が説明されるかどうかを判断できます。
個別値プロット
個別値プロットには、サンプルの個別値が表示されます。各円は1つの観測値を表しています。個別値プロットは、観測値数が比較的少なく、各観測値の効果も評価する必要がある場合に特に便利です。
解釈
個別値プロットを使用して、データの広がりを調べ、潜在的な外れ値を識別します。 個別値プロットは、サンプルサイズが50未満の場合に最適です。
- 歪んだデータ
-
データの広がりを調べて、データが歪んでいるかどうかを判断します。データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。
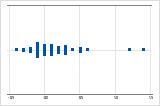
右方向の歪み
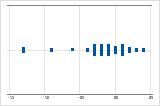
左方向の歪み
データが右方向に歪んだ個別値プロットは、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだ個別値プロットは、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。
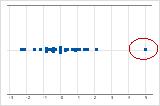
個別値プロットでは、異常に低いか高いデータ値で潜在的な外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
Q1
四分位数とは、並べられたデータのサンプルを4つの等しい部分に分ける、25%の第1四分位数(Q1)、50%の第2四分位数(Q2または中間値)、75%の第3四分位数(Q3)の3つの値です。
第1四分位数は第25百分位数であり、データの25%がこの値以下であることを示します。
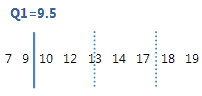
この順序付きデータで、第1四分位数(Q1)は9.5です。つまり、データの25%が9.5以下になります。
IQR
四分位間範囲(IQR)は、第1四分位数(Q1)と第3四分位数(Q3)の間の距離です。データの50%がこの範囲内に収まります。
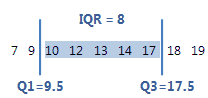
この順序付きデータでは、四分位間範囲は8(17.5–9.5 = 8)です。つまり、データの真ん中の50%が9.5~17.5です。
解釈
四分位間範囲を使用して、データの広がりを記述します。データの広がりが大きくなるにつれ、IQRは大きくなります。
最大値
最大値とは、最大のデータ値を指します。
このデータで、最大値は19です。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解釈
最大値を使用して、外れ値の可能性がある値またはデータ入力ミスを識別します。データの広がりを最も簡単に評価する方法の1つは、最小値と最大値を比較することです。データの中心、広がり、形状を検討する場合であっても、最大値が非常に大きい場合、極端な値の原因を調査してください。
中央値
中央値はデータセットの中間点です。この中間点の値は、観測値の半分がその値より上にあり、観測値の半分がその値より下にあるという点です。中央値は、観測値に順位付けし、順位付けされた順序での順位が[N + 1] / 2の観測値を検出することによって算定されます。観測値の数が偶数の場合、その中央値は、N / 2と[N / 2] + 1の順位で順位付けされる観測値の平均値です。

この順序付けされたデータの場合、中央値は13です。つまり、半数の値が13以下で、半数の値が13以上になっています。20に等しい観測値を追加すると、中央値は5番目の観測値(13)と6番目の観測値(14)の平均である13.5になります。
解釈
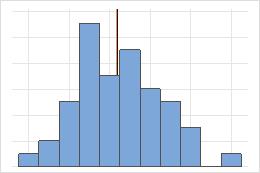
対称
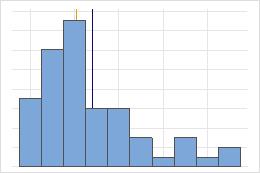
非対称
対称分布の場合、平均値(青い線)と中央値(オレンジ色の線)は非常によく似ているため、両方の線を簡単に確認することはできません。ただし、非対称分布は右側に歪んでいます。
最小値
最小値とは、最小のデータ値を指します。
このデータで、最小値は7です。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解釈
最小値を使用して、外れ値の可能性がある値またはデータ入力ミスを識別します。データの広がりを最も簡単に評価する方法の1つは、最小値と最大値を比較することです。データの中心、広がり、形状を検討する場合であっても、最小値が非常に小さい場合、極端な値の原因を調査してください。
範囲
範囲とは、サンプルの最も大きいデータ値と最も小さいデータ値の差です。範囲は、すべてのデータ値が含まれる区間を表します。
解釈
範囲を使用して、データの広がりを理解できます。範囲の値が大きい場合、データの広がりが大きいことを示します。範囲の値が小さい場合、データの広がりが小さいことを示します。範囲は2つのデータ値のみを使用して計算されるため、小さいデータセットを使用する場合に有用です。
Q3
四分位数とは、順序付きデータのサンプルを4つの等しい部分に分ける、25%の第1四分位数(Q1)、50%の第2四分位数(Q2または中間値)、75%の第3四分位数(Q3)の3つの値です。
第3四分位数は第75百分位数であり、データの75%がこの値以下であることを示します。
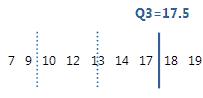
この順序付きデータで、第3四分位数(Q3)は17.5です。つまり、データの75%が17.5以下になります。
平均
平均値は、データの平均であり、すべての観測値の和を観測値の数で割って求められる値です。

解釈
データの中心を表す1つの値でサンプルを表すのに、平均を使います。多くの統計分析では、平均がデータ分布の中央の標準測度として使用されます。

対称

非対称
対称分布の場合、平均値(青い線)と中央値(オレンジ色の線)は非常によく似ているため、両方の線を簡単に確認することはできません。ただし、非対称分布は右側に歪んでいます。
平均の標準誤差
平均の標準誤差(平均のSE)では、同じ母集団から繰り返しサンプルを抽出した場合に得られるサンプル平均間の変動性が推定されます。平均の標準誤差はサンプル間の変動性を推定し、標準偏差は単一サンプル内の変動性を測定します。
たとえば、ランダムサンプルである312個の配達時間に基づいた平均配達時間は3.80日、標準偏差は1.43日であるとします。この数値から求められる平均の標準誤差は、0.08日(1.43を312の平方根で割ったもの)です。同じ母集団から同じサイズのランダムサンプルを複数抽出すると、異なるサンプル平均の標準偏差はおよそ0.08日になります。
解釈
平均の標準誤差を使用して、サンプル平均がどれだけ正確に母集団平均を推定するかを判断します。
平均の標準誤差の値が小さいと、母平均の推定値の精度が高くなります。通常、標準偏差が大きいと、平均の標準誤差が大きくなり、母平均の推定値の精度が低くなります。サンプルサイズが大きいと、平均の標準誤差が小さくなり、母平均の推定値の精度が高くなります。
Minitabは、平均の標準誤差を使用して信頼区間を計算します。
調整平均
値のうち最も高い5%と最も低い5%を除外したデータの平均。
調整平均は、極端に大きな値や小さな値が平均に与える影響を除外するために使用します。データに外れ値が含まれている場合、調整平均の方が平均よりも中心傾向の測定としては優れている場合があります。
累積個数
| 学年 | 計数 | 累積個数 | 計算 |
|---|---|---|---|
| 1 | 49 | 49 | 49 |
| 2 | 58 | 107 | 49 + 58 |
| 3 | 52 | 159 | 49 + 58 + 52 |
| 4 | 60 | 219 | 49 + 58 + 52 + 60 |
| 5 | 48 | 267 | 49 + 58 + 52 + 60 + 48 |
| 6 | 55 | 322 | 49 + 58 + 52 + 60 + 48 + 55 |
N*
サンプルにおける欠損値の数。欠損値の数は、欠損値記号*を含むセルを参照します。
| 合計数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
サンプルにおける非欠損値の数。
| 合計数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
合計数
列に含まれる観測値の合計数。欠損値の数と非欠損値の数の和を示すために使用します。
| 合計数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
累積パーセント
累積パーセントは、グループ変数の各グループのパーセンテージの累積和です。次の例では、グループ変数に行1、行2、行3、行4の4つのグループがあります。
| グループ(グループ変数) | パーセント | 累積パーセント |
|---|---|---|
| 行1 | 16 | 16 |
| 行2 | 20 | 36 |
| 行3 | 36 | 72 |
| 行4 | 28 | 100 |
パーセント
グループ変数の各グループの観測値の割合。次の例では、行1、行2、行3、行4の4つのグループがあります。
| グループ(グループ変数) | パーセント |
|---|---|
| 行1 | 16 |
| 行2 | 20 |
| 行3 | 36 |
| 行4 | 28 |
尖度
尖度は、分布の裾の正規分布からの逸脱の程度を示します。
解釈
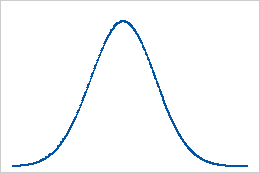
ベースライン:尖度の値が0
正規分布データによって、尖度のベースラインが確立されます。尖度の値が0の場合、データが完全に正規分布に従っていることを示します。0から大きく離れた尖度の値は、データが正規分布になっていないことを示す場合があります。
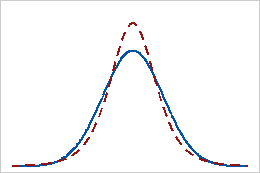
尖度の値が正
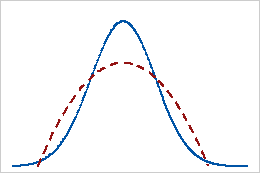
尖度の値が正の分布は、その分布に正規分布と比べて重い裾と鋭いピークがあることを示します。たとえば、t分布に従うデータの尖度は正の値になります。実線は正規分布を示し、点線は尖度の値が正の分布を示しています。
尖度の値が負
尖度の値が負の分布は、その分布に正規分布と比べて軽い裾があることを示します。たとえば、最初の形状パラメータと2番目の形状パラメータが2であるベータ分布に従うデータの尖度は負の値になります。実線は正規分布を示し、点線は尖度の値が負の分布を示しています。
歪度
歪度とは、データの非対称性を示す度合いです。
解釈
図A
図B
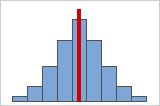
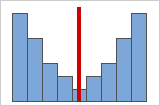
対称的な(歪みのない)分布
データが対称的になるほど、歪度の値は0に近づきます。図Aは、定義上、正規分布データは比較的小さい歪度を示すことを表しています。ここに示した正規分布データのヒストグラムの中央に直線を引くと、鏡に映したように両側が同じ形であることが簡単に分かります。ただし、歪みがないことだけで正規性を意味するわけではありません。図Bは、両側がやはり鏡に映したような形になっていますが、データは正規分布とは大きく異なる分布であることを表しています。
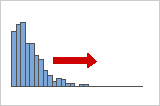
正に(右に)歪んでいる分布
正に歪んでいるデータ、または右に歪んでいるデータと呼ばれる理由は、分布の「裾」が右側に向かっており、歪度の値が0よりも大きくなる(正になる)からです。多くの場合、給与データはこのように歪みます。企業内の従業員の多くは給与が比較的低く、一方で、ごく少数の人たちの給与が非常に高いためです。
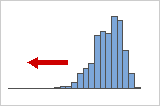
負に(左に)歪んでいる分布
左に歪んでいる、または負に歪んでいるデータと呼ばれる理由は、分布の「裾」が左側に向かっており、歪度の値が負になるからです。故障率のデータの多くは、左側に歪みます。電球を考えてみてください。すぐに焼き切れてしまう電球はごく少数で、大多数は非常に長持ちします。
変動係数
変動係数(CoefVar)とは、平均に対するデータの変動性を説明する広がりの測度です。変動係数は、値が単位を持たないように調整されます。この調整のおかげで、変動係数は単位が異なるデータや平均が著しく異なるデータの変動性を比較する場合に標準偏差の代わりに使用できます。
解釈
変動係数が大きいほど、データの広がりが大きくなります。
| 大きい容器 | 小さい容器 |
|---|---|
| 変動係数 = 100 * 0.4 カップ / 16 カップ = 2.5 | 変動係数 = 100 * 0.08 カップ / 1 カップ = 8 |
標準偏差
標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。記号σ(シグマ)は、母集団の標準偏差を示す場合によく使用されますが、sはサンプルの標準偏差を示す場合にも使用されます。多くの場合、工程に対してランダム(自然)な変動は雑音と呼ばれます。
標準偏差の単位はデータの単位と同じであるため、通常は、分散よりも解釈が簡単です。
解釈
標準偏差を使用して、平均からのデータの拡散程度を判断します。 標準偏差の値が高いほど、データの広がりが大きいことを示します。 正規分布の経験則によれば、値のおよそ68%が平均の1つの標準偏差の範囲内にあり、値の95%が2つの標準偏差の範囲内にあり、値の99.7%が3つの標準偏差の範囲内にあります。
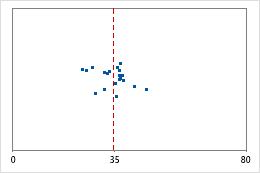
病院1

病院2
退院時間
管理者が、2つの病院の救急部門で処置を受けた患者の退院時間を追跡するとします。平均退院時間はほぼ同じ(35分)ですが、標準偏差には有意差があります。病院1の標準偏差はおよそ6です。平均すると、患者の退院時間は平均(点線)から約6分離れています。病院2の標準偏差はおよそ20です。平均すると、患者の退院時間は平均(点線)から約20分離れることになります。
分散
分散は、平均を中心としたデータの広がりを測定します。分散は標準偏差の二乗に等しくなります。
解釈
分散が大きいほど、データの広がりも大きくなります。
分散(σ2)は二乗した数量であるため、その単位も二乗されることになり、分散を実際に使用することは困難です。標準偏差は、データと同じ単位を使用するため、通常は解釈が簡単です。たとえば、バスの停留所での待ち時間のサンプルは、平均が15分で分散は9分2であるとします。分散は、データと同じ単位ではないため、多くの場合に平方根つまり標準偏差と一緒に表示されます。分散の9分2は、標準偏差の3分に相当します。
最頻値
最頻値とは、観測値のセットのうち、最も頻繁に発生する値のことです。Minitabには、最頻値と等しいデータ点の数も表示されます。
平均や中央値では計算が必要ですが、最頻値はデータセットの各値の発生回数を数えて判断します。
解釈
最頻値は、平均や中央値と一緒に使用して、データ分布の全体的な特徴を知ることができます。最頻値は、データの問題を識別するために使用することもできます。
たとえば、複数の最頻値がある分布では、サンプルに2つの母集団のデータが含まれていることを識別できます。データに2つの最頻値がある場合、分布は二峰性です。データに3つ以上の最頻値がある場合、分布はマルチモーダルです。
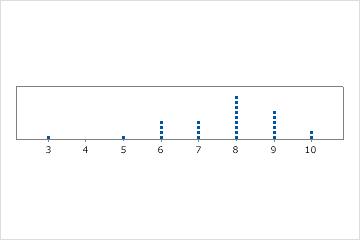
一峰性
最も頻繁に発生している最頻値(8)は1つのみです。
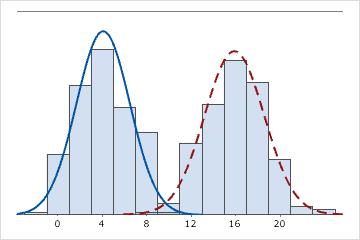
二峰性
2つの最頻値(4と16)があります。データは2つの異なる母集団を示していると思われます。
MSSD
MSSDとは、平方逐次的差分の平均です。MSSDは分散の推定値です。MSSDの使用法の1つとして、一連の観測値がランダムかどうかを検定する場合が考えられます。品質管理では、MSSDの使用法の1つとして、サブグループサイズが1の場合に分散を推定する場合が考えられます。
和
和とは、すべてのデータ値の合計です。和は、平均や標準偏差などの統計量計算にも使用されます。
平方和
未修正の平方和は、列の各値を平方し、その和を計算することで計算されます。たとえば、列にx1, x2, ... , xnが含まれている場合、平方和の計算は(x12 + x22 + ... + xn2)となります。修正された平方和とは異なり、未修正の平方和は誤差を含みます。データ値は最初に平均を引かずに二乗します。
