目的の方法または計算式を選択してください。
このトピックの内容
ピアソン相関係数
計算式
2変数間の線形関係の度合いを測定します。相関係数は、−1~+1の値を仮定します。一方の変数が増加するともう一方が減少する場合、相関係数は負になります。逆に、一方の変数が増加するにつれてもう一方の変数も増加する傾向にあるとき、相関係数は正の値になります。
変数xおよびyでは:
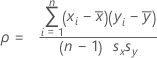
表記
| 用語 | 説明 |
|---|---|
 | 最初の変数のサンプル平均 |
| sx | 最初の変数のサンプル標準偏差 |
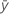 | 2番目の変数のサンプル平均 |
| sy | 2番目の変数のサンプル標準偏差 |
| n | 観測値数 |
ピアソン相関の信頼区間
ρの(1− α)100%の両面信頼区間は、(ρL, ρU)であり、ここでは、下限ρL、上限ρUが次のようになります。

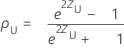
ここで、


表記
| 用語 | 説明 |
|---|---|
| r | 不明な相関のピアソンサンプル相関推定値、ρ |
| ρ | 相関係数 |
| n | 観測値数 |
スピアマンの相関係数
スピアマンの相関係数とp値を計算するには、データの順位でピアソン相関を実行します。同順位の応答値の順位は同順位の順位の平均となります。次の表は、2つのデータのサンプルの順位を示しています。
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| A | 順位A | B | 順位B |
| 45 | 4 | 23 | 1 |
| 78 | 6 | 25 | 3 |
| 24 | 3 | 25 | 3 |
| 51 | 5 | 25 | 3 |
| 13 | 1.5 | 34 | 6 |
| 13 | 1.5 | 30 | 5 |
AとBのスピアマンの相関係数は−0.678でp値は0.139です。この値は順位Aと順位Bの値のピアソン相関に基づいた相関係数およびp値とまったく同じです。
Minitabは、1つまたは両方の変数で欠損データが含まれる行を計算から除外します。両方の列の行数は同じでなければなりません。
スピアマン相関の信頼区間
ρの(1− α)100%の両面信頼区間は、(ρL、ρU)であり、ここでは、下限ρL、上限ρUが次のようになります。
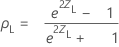
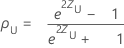
ここで、


ボネットとライト (2000) は、標準誤差で以下の調整を行うことを推奨してます。

表記
| 用語 | 説明 |
|---|---|
| r | 不明な相関のスピアマンサンプル相関推定値、ρ |
| ρ | 相関係数 |
| n | 変数のペアの欠損データを含まない行の数 |
p値
相関が0であるという検定の仮説は以下の通りです。
H0: ρ = 0 対 H1: ρ ≠ 0、ここではρは変数のペアの間のピアソン相関係数またはスピアマン相関係数です。
計算式
ピアソン相関係数とスピアマン相関係数の検定統計量の式は同じです。

p値は2 × P(T > t)、ここでは、Tは自由度n – 2のt分布に従います。
表記
| 用語 | 説明 |
|---|---|
| r | サンプル相関係数 |
| n | 観測値数 |
