ステップ1:行列プロットの変数間の関係を調べる
行列プロットを使用して、2つの連続変数の間の関係を調べます。また、関係の外れ値を探します。外れ値は、ピアソン相関係数の結果に大きな影響を与える可能性があります。
関係は線形関係、単調関係か、またはどちらにも当てはまらないかを判断します。以下は、相関係数が記述する形式の種類の例です。ピアソン相関係数は線形の形式に適しています。スピアマン相関係数は単調の形式に適しています。

関係なし
点はプロット上にランダムに落ちており、変数間に線形関係がないことを示しています。
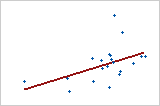
中程度の正の関係
線に近い点もあれば、遠い点もあり、変数間に中程度の線形関係しかないことを示しています。
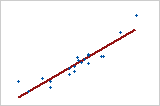
大きな正の関係
点は線に近く、変数間に強い線形関係があることを示しています。1つの変数が増加したとき他方の変数も増加するため、関係は正です。
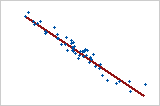
大きな負の関係
点は線に近く、変数間に強い負の関係があることを示しています。1つの変数が増加したとき他方の変数が減少するため、関係は負です。
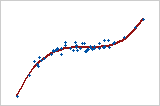
単調
単調関係では、変数が同じ相関方向に動く傾向がありますが、一定の割合とは限りません。線形関係では、変数は一定の割合で同じ方向に動きます。このプロットは、両方の変数が共に増大するが同じ率で増大しているわけではないことを示しています。この関係は単調ですが、線形ではありません。これらのデータのピアソン相関係数は0.843ですが、スピアマン相関の方が高く0.948です。
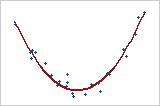
曲線2次
この例は曲線関係を示しています。変数間の関係が強くても、相関係数がゼロに近いこともあります。関係は線形でも、単調でもありません。
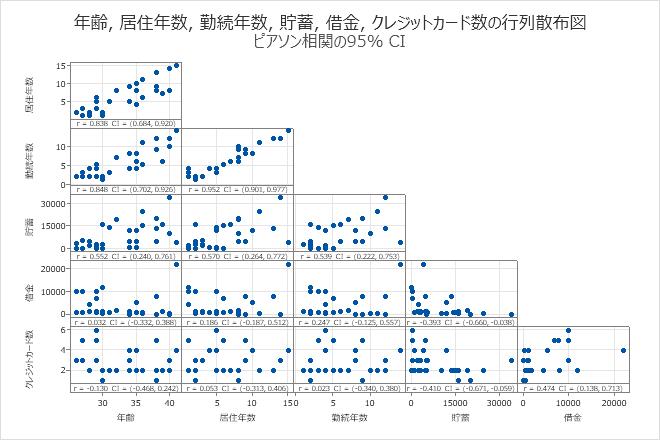
主要な結果:行列プロット
- 雇用状況と住所の間には、強い正の線形関係があります。
- クレジットカードと貯蓄の間には、弱い負の線形関係があります。
- 負債には調査の必要な外れ値があるようです。
ステップ2:変数間の相関係数を調べる
ピアソン相関係数を使用して、2つの連続変数の間の線形関係の強さと方向を調べます。
- 強度
-
相関係数の範囲は-1~+1の値です。係数の絶対値が大きいほど、変数間の関係は強まります。
ピアソン相関では、絶対値が1の場合、完璧な線形関係であることを示します。0に近い相関は、変数間に線形関係がないことを示します。 - 方向
-
相関係数の符号は関係の方向を示します。2つの変数がともに増加または減少する場合、係数は正で、相関を表す線の傾きが右上がりになります。一方の変数が増加するともう一方が減少する傾向にある場合、係数は負になり、相関を表す線の傾きが右下がりになります。
- 相関関係のみに基づいて、ある変数の変化が別の変数変化の原因となると結論付けることは決して適切ではありません。関係における因果関係の有無は、適切に制御された実験でのみ決定されます。
- ピアソンの相関係数は、極端なデータ値に対して非常に敏感です。データセットに含まれる他の値と非常に異なる値が1つあるだけでも、係数の値が大きく左右されます。極端な値の原因を識別する必要があります。データ入力や測定の誤差を修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
- ピアソン相関が低くても、変数間の関係がないとは限りません。変数には非線形関係があるかもしれません。
方法
| 相関の種類 | Pearson |
|---|---|
| 使用中の行数 | 30 |
相関
| 年齢 | 居住年数 | 勤続年数 | 貯蓄 | 借金 | |
|---|---|---|---|---|---|
| 居住年数 | 0.838 | ||||
| 勤続年数 | 0.848 | 0.952 | |||
| 貯蓄 | 0.552 | 0.570 | 0.539 | ||
| 借金 | 0.032 | 0.186 | 0.247 | -0.393 | |
| クレジットカード数 | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
主要な結果:ピアソン相関
- 住所と年齢、0.838
- 雇用状況と年齢、0.848
- 雇用状況と住所、0.952
- 負債と貯蓄、−0.393
- クレジットカードと年齢、−0.130
- クレジットカードと貯蓄、−0.410
