ある銀行では、ローン申請者を、収入、学歴、年齢、現住所での居住年数、現職での勤続年数、貯蓄、負債、およびクレジットカード数の8項目で審査します。担当責任者は、このデータをグループ化して報告する最良の方法を決定するためにデータを分析しようとしています。そこで、30人のローン申請者についてこの情報を収集しました。
銀行の管理者は、ピアソン相関を使用して変数の各ペア間の線形関係の強さと方向を調べます。
- 標本データを開く、 ローン申請者.MWX.
- を選択します。
- 変数に、年齢 居住年数 勤続年数 貯蓄 借金 「クレジットカード数」を入力します。
- グラフをクリックします。
- プロットに表示する統計量で、相関と区間を選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
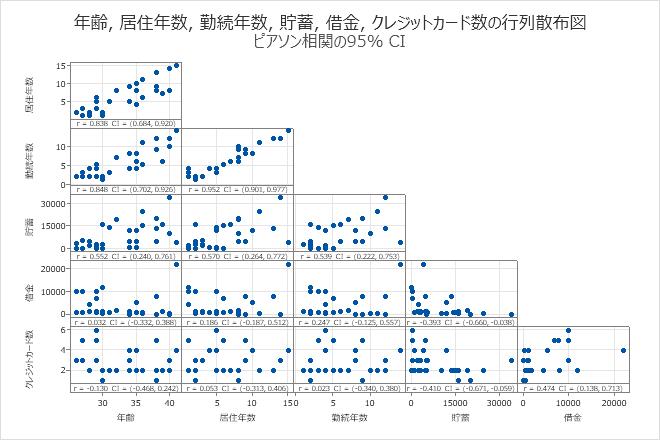
行列プロットを使用して、変数のすべての組み合わせにおける関係を視覚的に評価します。関係は線形、単調関係であるか、またはどちらにも当てはまらないかもしれません。
- 最も高いピアソン相関係数は、雇用状況と住所の間にあります。この0.952の値は変数間の正の関係を表しています。雇用状況が増加すると、住所も増加します。95%の信頼区間は0.901~0.977です。
- クレジットカードと貯蓄の間のピアソン相関係数は–0.410です。クレジットカードの枚数が増えると、貯蓄が減る傾向にあります。95%の信頼区間範囲は–0.671~–0.059です。
また、行列プロットを使用して、結果に大きな影響を与え得る外れ値を探します。例えば、行6には変数間の相関に影響を与えそうな極端なデータ点が含まれています。この例は、負債と年齢プロットで見ることができます。
通常、相関が強いと、信頼区間が狭くなります。例えば、クレジットカードと年齢の相関は弱く、95%信頼区間は-0.468~0.242です。
相関: 年齢, 居住年数, 勤続年数, 貯蓄, 借金, クレジットカード数
方法
| 相関の種類 | Pearson |
|---|---|
| 使用中の行数 | 30 |
相関
| 年齢 | 居住年数 | 勤続年数 | 貯蓄 | 借金 | |
|---|---|---|---|---|---|
| 居住年数 | 0.838 | ||||
| 勤続年数 | 0.848 | 0.952 | |||
| 貯蓄 | 0.552 | 0.570 | 0.539 | ||
| 借金 | 0.032 | 0.186 | 0.247 | -0.393 | |
| クレジットカード数 | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
