Minitab® サポート

2サンプルの分散の方法と計算式

Minitab についての 詳細
目的の方法または計算式を選択してください。

このトピックの内容

サンプル統計量

Minitabは、両方のサンプルの平均、標準偏差、および分散を計算します。

計算式

標準偏差は、分散の平方根に等しくなります。

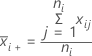
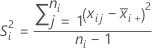
表記

用語説明
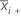サンプルiの平均
S2i サンプルiの分散
Xij i番目のサンプルのj番目の測定値
ni サンプルiのサイズ

バランス型計画を使用したBonettの方法の検定

検定統計量の計算式

n1 = n2の場合、検定統計量はZ2となります。帰無仮説ρ = ρ0が真の場合、Z2は自由度が1のカイ二乗分布として分布されます。Z2は次のように求められます。

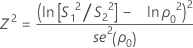
ここで、se(ρ0)は併合尖度の標準誤差で、次のように求められます。

ここで、ri = ( ni - 3) / ni、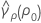は併合尖度で、次のように求められます。

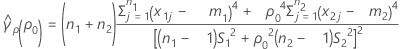
se2(ρ0)は、次のように個別のサンプル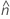の尖度値に関連して表現することもできます。

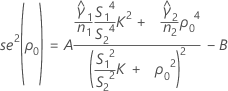
ここで、

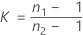
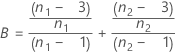
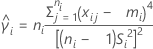
p値の計算式

z2をデータから得られるZ2の値とします。帰無仮説H0: ρ = ρ0で、Zは標準正規分布として分布されます。したがって、対立仮説（H1）のp値は次のように求められます。

仮説 p値
H1: ρ0 ≠ ρ0 P = 2P(Z > |z|)
H1: ρ0 > ρ0 P = P(Z > z)
H1: ρ0 < ρ0 P = P(Z < z)

表記

用語説明
Siサンプルiの標準偏差
ρ母標準偏差の比
ρ0母標準偏差の仮説比
α検定の有意水準 = 1 - (信頼水準 / 100)
niサンプルiの観測値数
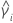サンプルiの尖度値
Xijサンプルiのj番目の観測値
miサンプルiの調整平均で、調整比率は

アンバランス型計画を使用したBonettの方法の検定

計算式

n1 ≠ n2の場合、検定統計量はありません。p値は、信頼区間の手順を逆にすることで計算されます。この検定のp値は次のように求められます。

P = 2 min (αL, αU)

ここで、αLは次の条件を満たすαの最小値です。
αUは次の条件を満たすαの最小値です。

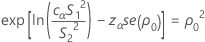
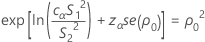
ここで、cαは等化定数（下記参照）で、se(ρ0)は併合尖度の標準誤差であり、次のように求められます。

ここでri = (ni - 3) / ni、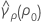は併合尖度で、次のように求められます。

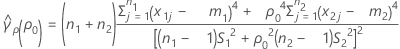
se(ρ0)は、個別のサンプルの尖度値に関連させて表現することもできます。詳細については、バランス型計画を使用したBonettの方法の検定のセクションを参照してください。

等化定数

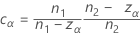
アンバランス型計画で等しくない裾部による誤差の確率の影響を削減するために、定数cαが小サンプル調整として含まれています。cαの値は次のように求められます。

計画がバランス型で、サンプルサイズの増加とともにその影響を無視できるようになると、定数は0とみなせます。

αLとαUの検出

αLとαUの検出は、関数L(z , n1 , n2 , S1 , S2 )およびL(z , n2 , n1 , S2 , S1 )の累乗根の検出と等価です。ここで、L(z , n1 , n2 , S1 , S2)は次のように求められます。

次のように定義します。
n1 < n2の場合、次の操作を行います。
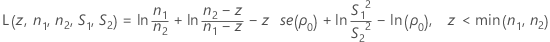
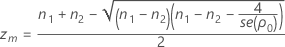
  • zmを計算して、L(z, n1, n2, S1, S2)を評価します。
    • L(zm) 0の場合、次の区間でL(z, n1, n2, S1, S2)の累乗根zLを見つけます。そしてαL = P( Z > zL)を計算します。
    • L(zm) > 0の場合、関数L(z , n1, n2, S1, S2)には累乗根がなく、αL = 0となります。
n1 > n2の場合、次の操作を行います。
  • L(0, n1, n2, S1, S2) = ln (S12 / S22)を計算します。
    • L(0, n1, n2, S1, S2) 0の場合、区間[0, n2)でL(z, n1, n2, S1, S2)の累乗根z0を見つけます。
    • L(0, n1, n2, S1, S2) < 0の場合、次の区間で累乗根zLを見つけます。。
  • αL = P( Z > zL)を計算します。

αUを計算するには、関数L(z, n1, n2, S1, S2)の代わりに関数L(z, n2, n1, S2, S1)を使用して前述のステップを行います。

表記

用語説明
Siサンプルiの標準偏差
ρ母標準偏差の比
ρ0母標準偏差の仮説比
α検定の有意水準 = 1 - (信頼水準 / 100)
zα標準正規分布のα上側百分位数点
niサンプルiの観測値数
Xijサンプルiのj番目の観測値
miサンプルiの調整平均で、調整比率は

Bonettの方法の信頼区間

計算式

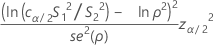
信頼区間は検定手順を逆にして得られます。具体的には、以下の等式を解いてρの値を求めます。

ここでは、cα/2が等化器定数 (以下に記述) 、se(ρ)が併合尖度の標準偏差 (以下に記述) です。典型的には、この等式には解L < S1 / S2および解U > S1 / S2の2つがあります。Lは下側信頼限界、Uは上側信頼限界です。詳細は、ボネットの方法すなわち、シミュレーションやボネットの方法に関する情報が記載された白書をご覧ください。

分散比の信頼限界は標準偏差比の信頼限界を2乗して得られます。

等化器定数

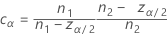
アンバランス型計画で等しくない裾部による誤差の確率の影響を削減するために、定数cαが小サンプル調整として含まれています。cαの値は次のように求められます。

計画がバランス型で、サンプルサイズの増加とともにその影響を無視できるようになると、定数は0とみなせます。

併合尖度の標準偏差

se(ρ)は併合尖度の標準偏差で、次のように求められます。

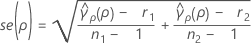
ここでは、ri = (ni - 3) / niおよび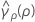 は併合尖度の標準偏差で、次のように求められます。

se(ρ)は、個別のサンプルの尖度値に関連させて表現することもできます。詳細については、バランス型計画を使用したBonettの方法の検定のセクションを参照してください。

表記

用語説明
αテスト = 1 - (信頼水準 / 100)の有意水準
Siサンプルiの標準偏差
ρ母集団標準偏差の比率
zα/2標準正規分布のα / 2番目の上側百分位数点
niサンプルiに含まれる観測数
Xijサンプルiに含まれるj番目の観測値
miサンプルiの調整平均、調整比率は、

Leveneの方法の検定

計算式

Leveneの検定は連続データに適しています。Leveneの検定は要約データでは行えません。

Leveneの検定でσ1 / σ2 = ρという帰無仮説を検定するために、Minitabは値Z1jおよびρZ2jで一元配置分散分析を実行します（ここで、j = 1, …, n1またはn2）。

Leveneの検定統計量は、得られた分散分析表のF統計量の値に等しくなります。Leveneの検定p値は、この分散分析表のp値に等しくなります。

  • H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
  • M.B. Brown and A.B. Forsythe (1974). "Robust Tests for the Equality of Variance," Journal of the American Statistical Association, 69, 364–367.

自由度

帰無仮説のもとで、検定統計量は自由度がDF1およびDF2のF分布に従います。

DF1 = 1

DF2 = n1 + n2 – 2

表記

用語説明
Zij|Xi j – η i|
用語説明
j1, 2, …, ni
ii1, 2
Xij個々の観測値
ηiサンプルiの中央値
σ1第1母集団の標準偏差
σ2第2母集団の標準偏差
n1第1サンプルのサイズ
n2第2サンプルのサイズ

Leveneの方法の信頼区間

計算式

連続データの場合、Minitabは次の計算式を使用して、母標準偏差間の比（ρ）の信頼限界を計算します。母分散間の比の限界を求めるには、下の値を平方します。

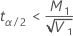[比 ≠ 仮説比]の対立仮説を指定した場合、ρの100(1–α)%信頼区間は次のように求められます。

  • の場合、下限 =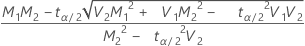

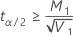    の場合、下限は存在しません

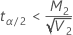  • の場合、上限 =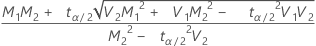

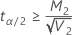    の場合、上限は存在しません

[比 < 仮説比]の対立仮説を指定した場合、ρの100(1 – α)%上側信頼境界値は次のように求められます。

  • の場合、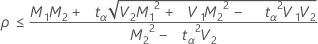

  • の場合、上限は存在しません
[比 > 仮説比]の対立仮説を指定した場合、ρの100(1 – α)%上側信頼境界値は次のように求められます。

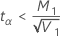  • の場合、

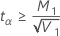  • の場合、下限は存在しません

表記

用語説明
t α n1 + n2 – 2 自由度の t 分布の α 臨界値
ηiサンプルiの中央値
Zijここで、j = 1, 2, ... , ni、i = 1, 2であり、Xijは個別の観測値です
MiZijの平均
Si2Zijのサンプル分散
vi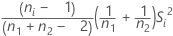
ρσ1 / σ2
n1第1サンプルのサイズ
n2第2サンプルのサイズ

F検定の方法の検定

F検定は正規データに適しています。F検定を使用してσ1 / σ2 = ρという帰無仮説を検定するために、Minitabは次の計算式を使用します。

検定統計量の計算式

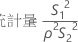
自由度の計算式

帰無仮説のもとで、F統計量は自由度がDF1およびDF2のF分布に従います。

DF1 = n1 – 1

DF2 = n2 – 1

p値の計算式

p値の計算は、次のように対立仮説によって異なります。
  • 「より小さい」対立仮説を使用した片側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値以下のF統計量が得られる確率に等しくなります。
  • 比が1より小さい両側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値より小さいF曲線の下の部分の2倍に等しくなります。
  • 比が1より大きい両側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値より大きいF曲線の下の部分の2倍に等しくなります。
  • 「より大きい」対立仮説を使用した片側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値以上のF統計量が得られる確率に等しくなります。

表記

用語説明
ρσ1 / σ2
σ1第1母集団の標準偏差
σ2第2母集団の標準偏差
S21第1サンプルの分散
S22第2サンプルの分散
n1第1サンプルのサイズ
n2第2サンプルのサイズ

F検定の方法の信頼区間

データが正規分布に従う場合、Minitabは次の計算式を使用して、母標準偏差間の比（ρ）の信頼境界値を計算します。母分散間の比の境界値を求めるには、下の値を平方します。

計算式

「等しくない」対立仮説を指定した場合、ρの100(1 – α)%信頼区間は次のように求められます。

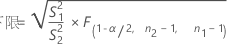
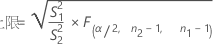
「次より小さい」対立仮説を指定した場合、ρの100(1 – α)%上側信頼境界値は次のように求められます。

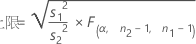
「次より大きい」対立仮説を指定した場合、ρの100(1 – α)%下側信頼境界値は次のように求められます。

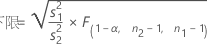
表記

用語説明
S1第1サンプルの標準偏差
S2第2サンプルの標準偏差
ρσ1 / σ2
n1第1サンプルのサイズ
n2第2サンプルのサイズ
F(α/2, n2–1, n1–1)自由度n2–1およびn1–1のF分布のα/2棄却値。
Copyright © 2026 Minitab, LLC. All rights Reserved.