ある医療コンサルタントが2つの病院の患者満足度評価を比較しようとしています。コンサルタントは各病院の20人の患者から評価を収集します。
コンサルタントは、2病院の患者満足度の標準偏差の差があるかを調べるために2サンプルの分散検定を実行します。
- 標本データを開く、 病院比較.MWX.
- を選択します。
- ドロップダウンリストから、両方のサンプルが1つの列にあるを選択します。
- サンプルに評価を入力します。
- サンプルIDに病院を入力します。
- OKをクリックします。
結果を解釈する
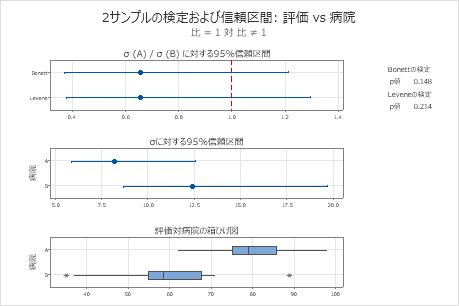
帰無仮説では、標準偏差間の比が1であると仮定します。p値がどちらも有意水準(αまたはアルファで示される)0.05より大きいため、コンサルタントは帰無仮説を棄却できません。コンサルタントには2つの病院の標準偏差が異なると結論付けるのに十分な証拠がありません。
方法
| σ₁: 病院 = Aの場合の評価の標準偏差 |
|---|
| σ₂: 病院 = Bの場合の評価の標準偏差 |
| 比: σ₁/σ₂ |
| BonettおよびLeveneの方法は、どの連続分布でも有効です。 |
記述統計量
| 病院 | N | 標準偏差 | 分散 | σに対する95%信頼区間 |
|---|---|---|---|---|
| A | 20 | 8.183 | 66.958 | (5.893, 12.597) |
| B | 20 | 12.431 | 154.537 | (8.693, 19.709) |
標準偏差の比
| 推定比 | Bonettを使用した比に対する 95%信頼区間 | Leveneを使用した比に対する 95%信頼区間 |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
検定
| 帰無仮説 | H₀: σ₁ / σ₂ = 1 |
|---|---|
| 対立仮説 | H₁: σ₁ / σ₂ ≠ 1 |
| 有意水準 | α = 0.05 |
| 方法 | 検定統計量 | DF1 | DF2 | p値 |
|---|---|---|---|---|
| Bonett | 2.09 | 1 | 0.148 | |
| Levene | 1.60 | 1 | 38 | 0.214 |