目的の方法または計算式を選択してください。
標準偏差
標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。サンプル標準偏差は、サンプル分散の平方根に等しくなります。
列にx1, x2,..., xNが含まれていて、平均が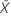 の場合、標準偏差は次のように求められます。
の場合、標準偏差は次のように求められます。

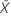 の場合、標準偏差は次のように求められます。
の場合、標準偏差は次のように求められます。

表記
| 用語 | 説明 |
|---|---|
| xi | サンプルのi番目の観測値 |
 | サンプル平均 |
| S | サンプル標準偏差 |
| n | サンプルサイズ |
分散
分散は、平均を中心としたデータの広がり方を測定します。分散は、標準偏差の二乗に等しくなります。
計算式
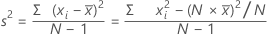
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の観測値 |
 | 観測値の平均 |
| N | 非欠損観測値の数 |
カイ二乗法の信頼区間と境界
この方法は、データが正規分布の場合に使用します。この方法は、サンプルサイズが非常に大きい場合でも、非正規データでは不正確になります。
信頼区間
母標準偏差の100(1 - α)%信頼区間は次のように求められます。
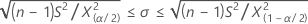
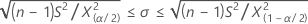
母分散の100(1 - α)%信頼区間は次のように求められます。


信頼境界
片側検定を指定した場合、Minitabでは対立仮説の方向に従い、片側の100(1–α)%信頼境界が計算されます。
- 「次より大きい」対立仮説を指定した場合、母標準偏差の100(1–α)%下限は次のように求められます。

母分散の100(1–α)%下限は次のように求められます。

- 「次より小さい」対立仮説を指定した場合、母標準偏差の100(1–α)%上限は次のように求められます。

母分散の100(1–α)%上限は次のように求められます。

表記
| 用語 | 説明 |
|---|---|
| α | 100(1 – α)%信頼区間のα水準 |
| n | サンプルサイズ |
| S2 | サンプル分散 |
| Χ2(p) | 自由度が(n – 1)のカイ二乗分布の上側の第100p百分位数点 |
| σ | 母標準偏差の真の値 |
| σ2 | 母分散の真の値 |
Bonettの方法の信頼区間と境界
この方法は連続データ(正規または非正規)に使用します。1
信頼区間
母標準偏差の100(1-α)%信頼区間は次のように求められます。


母分散の100(1-α)%信頼区間は次のように求められます。


信頼境界
片側検定を指定した場合、Minitabでは対立仮説の方向に従い、片側の100(1–α)%信頼境界が計算されます。
-
「次より大きい」対立仮説を指定した場合、母標準偏差の100(1–α)%下限は次のように求められます。
 母分散の近似的な100(1- a)%下限は次のように求められます。
母分散の近似的な100(1- a)%下限は次のように求められます。
-
「次より小さい」対立仮説を指定した場合、母標準偏差の近似的な100(1 – α)%上限は次のように求められます。
 母分散の近似的な100(1- a)%上限は次のように求められます。
母分散の近似的な100(1- a)%上限は次のように求められます。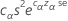
表記
| 用語 | 説明 |
|---|---|
| α | 1 – 信頼水準 / 100 |
| cα/2 | n / (n – zα/2) |
| cα | n / (n – zα ) |
| s2 | サンプル分散の観測値 |
| zα/2 | 1 – α/2における標準正規分布の逆累積確率。nがzα/2以下の場合、MinitabではBonettの信頼区間が計算されません。 |
| zα | 1 – αにおける標準正規分布の逆累積確率。nがzα 以下の場合、MinitabではBonettの信頼区間が計算されません。 |
| se |  |
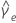 | 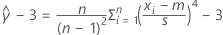 = 推定過剰尖度 = 推定過剰尖度 |
| m | 調整比率が に等しい調整平均。nが5以下の場合、m = サンプル平均 に等しい調整平均。nが5以下の場合、m = サンプル平均 |
| σ | 母標準偏差の真の値 |
| σ2 | 母分散の真の値 |
カイ二乗法の仮説検定
この方法は、データが正規分布の場合に使用します。この方法は、サンプルサイズが非常に大きい場合でも、非正規データに対して不正確になります。
計算式
仮説検定では、それぞれの対立仮説について次のp値式を使用します。
H1: σ2 > σ02: p値 = P(Χ2 ≥ x2)
H1: σ2 < σ02: p値 = P(Χ2 ≤ x2)
H1: σ2 ≠ σ02: p値 = 2 × min{P(Χ2 ≤ x2), P(Χ2 ≥ x2)}
表記
| 用語 | 説明 | ||||||
|---|---|---|---|---|---|---|---|
| σ2 | 母分散の真の値 | ||||||
| σ02 | 母分散の仮説値 | ||||||
| Χ2 | σ2 = σ02の場合、自由度が(n – 1)のカイ二乗分布に従います | ||||||
| x2 | 
|
Bonettの方法の仮説検定
この方法は連続データ(正規または非正規)に使用します。
計算式
Bonettの手順は検定統計量に関連付けられていません。ただし、Minitabは信頼限界によって定義される棄却域を使用してp値を計算します。
両側仮説の場合、p値は次のように求められます。
p = 2 × min(αL, αU)
- 片側の「次より小さい」対立仮説の場合、p値は表記のα/2をαに置き換えた後でαUとして計算されます。
- 片側の「次より大きい」対立仮説の場合、p値は表記のα/2をαに置き換えた後でαLとして計算されます。
表記
| 用語 | 説明 | ||||||
|---|---|---|---|---|---|---|---|
| σ02 | 仮説分散 | ||||||
| αL | 次の式の最小解α
 | ||||||
| αU | 次の式の最小解α
 | ||||||
| cα/2 | n / (n – zα/2) | ||||||
| α | 1 – 信頼水準 / 100 | ||||||
| s2 | サンプル分散の観測値 | ||||||
| zα/2 | 1 – α/2における標準正規分布の逆累積確率。nがzα/2以下の場合、MinitabではBonettの信頼区間が計算されません。 | ||||||
| se | 
|
1 D.G. Bonett (2006). "Approximate confidence interval for standard deviation of nonnormal distributions" , Computational Statistics & Data Analysis, 50, 775-782.