統計量
| 用語 | 説明 |
|---|---|
| 出現率 |
 |
| 出現平均 |
 |
率は、観測の長さの単位あたりの平均出現件数に等しくなります。平均は、サンプル全体の平均出現件数です。長さが1に等しい場合、率と平均は等しくなります。
正確検定のp値
計算式
- H1: λ > λ0: p値 = P(S ≥ s | λ = λ0)。ここで、Sは平均nλ0tのポアソン分布。
- H1: λ < λ0: p値 = P(S ≤ s | λ = λ0)。ここで、Sは平均nλ0tのポアソン分布。
- H1: λ ≠ λ0: Minitabは次のように尤度比検定を使用します。
関数G(s)を定義します。この関数では、ポアソン工程に含まれる出現総数sに関して尤度比検定を表現します。

- 0 ≤ s < nλ0tの場合、区間(nλ0t, enλ0t]でyについて式G(y) = G(s)を解きます。
p値 = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- s = nλ0tの場合、
p値 = 1.00
- nλ0t < s ≤ enλ0tの場合、区間[0, nλ0t)でyについて式G(y) = G(s)を解きます。
p値 = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- s > enλ0tの場合、検定は片側で、
p値 = P(S ≥ s | λ = λ0)となります
ここで、Sは平均nλ0tのポアソン分布です。
- 0 ≤ s < nλ0tの場合、区間(nλ0t, enλ0t]でyについて式G(y) = G(s)を解きます。
表記
| 用語 | 説明 |
|---|---|
| s | ポアソン工程内の出現総数 |
| t | 観測の「長さ」 |
| λ0 | 母集団率パラメータの仮説値 |
| λ | 母集団率パラメータの真の値 |
| n | サンプルサイズ |
| e(E) | 2.71828(近似値) |
正確検定の信頼区間と信頼境界値
信頼区間
ポアソン工程の出現率の正確な100(1 – α)%信頼区間は次のように求められます。
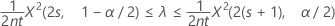
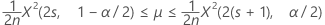
信頼境界
片側検定を指定した場合、Minitabでは対立仮説の方向に従い、片側の100(1 – α)%信頼境界が計算されます。
-
「次より大きい」対立仮説を指定した場合、率の正確な100(1 – α)%下限は次のように求められます。
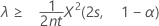
平均の正確な100(1 – α)%下限は次のように求められます。
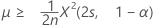
-
「次より小さい」対立仮説を指定した場合、率の正確な100(1 – α)%上限は次のように求められます。
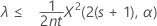
平均の正確な100(1 – α)%上限は次のように求められます。
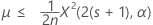
表記
| 用語 | 説明 |
|---|---|
| s | ポアソン工程内の出現総数 |
| t | 観測の「長さ」 |
| λ | 母集団率の真の値 |
| μ | 母平均の真の値 |
| Χ2(p, x) | 自由度pのΧ2分布の上側x百分位数点(0 < x < 1) |
| α | 100(1–α)%信頼区間のα水準 |
| n | サンプルサイズ |
正規近似法のp値
総出現数が10より大きい場合、正規近似法が有効です。
計算式
1サンプルポアソン率の正規近似に基づいた仮説検定では、それぞれの対立仮説について次のp値式を使用します。


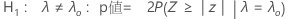
表記
| 用語 | 説明 |
|---|---|
| Z | 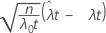 |
| t | 観測の「長さ」 |
| λ 0 | 母集団率パラメータの仮説値 |
| λ | 母集団率パラメータの真の値 |
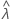 | サンプル率統計量の観測値 |
| n | サンプルサイズ |
正規近似の信頼区間と信頼境界
信頼区間
ポアソン工程の出現率の正規近似に基づいた100(1 – α)%信頼区間は次のように求められます。
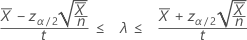
「長さ」の値を指定すると、Minitabには平均出現数の信頼区間も表示されます。この信頼区間は次のように求められます。
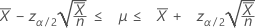
信頼境界
片側検定を指定すると、Minitabでは対立仮説の方向に従い、片側の100(1 – α)%信頼境界が計算されます。-
「次より大きい」対立仮説を指定した場合、率の正確な100(1 – α)%下限は次のように求められます。
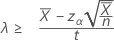
「長さ」の値を指定すると、平均の正確な100(1-α)%下限は次のように求められます。
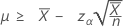
-
「次より小さい」対立仮説を指定した場合、率の正確な100(1 – α)%上限は次のように求められます。
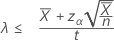
「長さ」の値を指定した場合、平均の正確な100(1 – α)%上限は次のように求められます。
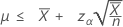
表記
| 用語 | 説明 |
|---|---|
| s | ポアソン工程内の出現総数 |
| t | 観測の「長さ」 |
| λ | 母集団率の真の値 |
| μ | 母平均の真の値 |
| Zx | 標準正規分布のx番目の上側百分位数点(0 < x < 1) |
| α | 100(1–α)%信頼区間のα水準 |
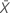 | サンプル内の平均出現件数 |
| n | サンプルサイズ |
