このトピックの内容
調整されたBlakerの正確な信頼区間と検定方法
対立仮説の分析設定では、両側信頼区間を生成するか、片側信頼限界を生成するかを指定します。代替仮説が小さいか大きい場合、解析は片側信頼限を導き出します。片側信頼限界の場合、分析ではクロッパー・ピアソンの厳密法が使用されます。
両側対立仮説の場合、分析は両側信頼区間を生成します。Minitab Statistical Softwareでの分析では、KlaschkaとReiczigelのアルゴリズムを使用して信頼区間とp値を生成します。1このメソッドの名前は、調整された Blaker exact メソッドです。この数値アルゴリズムは計算が速く、一般的に一致する信頼区間と検定を生成します。調整されたブレイカー信頼区間も正確で、枝分かれしています。
調整済みブレイカー厳密法では、事象の比率の両側信頼区間が生成され、p ≠ p0の対立仮説の p 値が生成されます。Blaker23 は、正確確率検定のp値関数を反転することにより、正確な両側信頼区間を提供します。Clopper-Pearson区間は幅が広く、常にBlaker信頼区間が含まれます。Blaker exact メソッドの間隔は入れ子になっています。この特性は、信頼水準が高い信頼区間には、信頼水準が低い信頼区間が含まれることを意味します。たとえば、正確な両側 Blaker 95% 信頼区間には、対応する 90% 信頼区間が含まれています。
Minitab Statistical Softwareが使用するアルゴリズムは、Blakerの元の厳密法の2つの制限を克服しています。1つの制限は、信頼区間を計算する数値アルゴリズムが、特にサンプルサイズが大きい場合に遅くなることです。もう1つの制限は、一部のデータでは、元のBlakerの正確確率法では、p値が信頼水準に対応する有意水準よりも小さい場合に、仮説された比率をカバーする区間が生成されることです。この制限は、p 値が信頼水準に対応する有意水準よりも大きい場合に、信頼区間に仮説の比率が含まれていない場合にも発生します。
Clopper-Pearsonの正確信頼区間法
区間 (PL, PU) は、 pの両側 100(1 – α)% 信頼区間です。サンプルにイベントがない場合、下限は0です。サンプルにイベントのみがある場合、上限は1となります。
片側下限
計算式

表記
| 用語 | 説明 |
|---|---|
B(1 −  ; a, b) ; a, b) | 下側、1 -  パラメータ A および Bを持つベータ分布のパーセンタイル パラメータ A および Bを持つベータ分布のパーセンタイル |
| x | 事象数 |
| n | 試行回数 |
片側上限
計算式

表記
| 用語 | 説明 |
|---|---|
B( ; a, b) ; a, b) | 上側  パラメータ A および Bを持つベータ分布のパーセンタイル パラメータ A および Bを持つベータ分布のパーセンタイル |
| x | 事象数 |
| n | 試行回数 |
両側下限
注
Clopper-Pearson方式の両側制限はコマンドラインでのみ利用可能です。
計算式
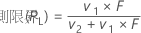
表記
| 用語 | 説明 |
|---|---|
| v1 | 2x |
| v2 | 2(n – x + 1) |
| x | 事象数 |
| n | 試行回数 |
| F | 自由度がv1およびv2のF分布の下限α/2の点 |
両側上限
注
Clopper-Pearson方式の両側制限はコマンドラインでのみ利用可能です。
計算式
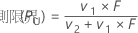
表記
| 用語 | 説明 |
|---|---|
| v1 | 2(x + 1) |
| v2 | 2(n – x) |
| x | 事象数 |
| n | 試行回数 |
| F | 自由度がv1およびv2のF分布の上限α/2の点 |
Clopper-Pearsonの正確信頼区間に対応する検定
計算式
- Ha: p ≠ p0
- p値 =
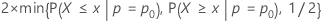
- Ha: p > p0
- p 値 = P{ X ≥ x | p = po}
- Ha: p < p0
- p 値 = P{ X ≤ x | p = po}
表記
| 用語 | 説明 |
|---|---|
| p0 | 仮説の比率 |
| n | 試行回数 |
| p | 事象の確率 |
| x | 事象数 |
ウィルソンスコア信頼区間法
ウィルソン4 スコア検定を反転して、Minitab Statistical SoftwareがWilsonスコア信頼区間と名付けた信頼区間を取得します。ウィルソンスコア区間には2つの形式があり、1つは連続性補正なし、もう1つは連続性補正ありです。補正なしの区間のカバレッジは、名義信頼水準を下回ることがあります。補正を伴う区間の実際の信頼水準は、少なくとも名義信頼水準です。どちらの方法でも、サンプルにイベントがない場合、下限は0です。サンプルにイベントのみが含まれる場合、上限は 1 です。
連続性補正なしの区間
両側100(1 – α)%信頼区間の計算式は次のとおりです。
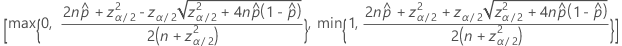
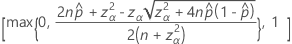
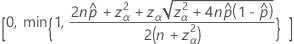
連続性補正の間隔
両側100(1 – α)%区間の下限は、次の式になります。
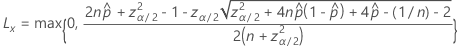
両側100(1 – α)%区間の上限は、次の式になります。
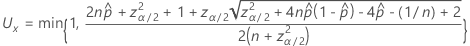
片側100(1 – α)%の下限には、次の式があります。
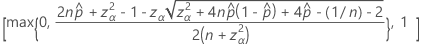
片側100(1 – α)%の上限には、次の式があります。
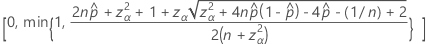
表記
| 用語 | 説明 |
|---|---|
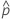 | 観測された確率、 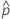 = x / n = x / n |
| x | 事象数 |
| n | 試行回数 |
| zγ | γにおける標準正規分布の上側百分位点 |
| α | 1 – 信頼水準/100 |
スコアテスト
導通補正なしの方法
ウィルソン スコア信頼区間と正規近似法 (Web アプリ) に対応する検定は、既知のスコア検定です。スコアテストの統計量には、次の式があります。
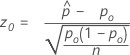
- Ha: p ≠ p0
- p値 =

- Ha: p > p0
- p値 =

- Ha: p < p0
- p値 =

導通補正法
連続性補正を伴う手順の検定統計量とp値は、対立仮説によって異なります。
- Ha: p ≠ p0
-

- Ha: p > p0
-

- Ha: p < p0
-

表記
| 用語 | 説明 |
|---|---|
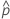 | 観測された確率、x/n |
| x | 事象数 |
| n | 試行回数 |
| p0 | 仮説の比率 |
 | Yにおける標準正規分布の累積分布関数 |
Agresti-Coull信頼区間と試験方法
信頼区間
Agresti と Coull5 は、カバレッジ特性を改善する信頼区間の Wald 法を調整します。両側95%信頼区間の場合、調整では2つの事象と2つの非事象がほぼ加算され、Wald信頼区間の式から信頼区間が計算されます。サンプルにイベントがない場合、下限は0です。サンプルにイベントのみが含まれる場合、上限は 1 です。
両側 100(1 – α)% 区間の計算式は次のとおりです。
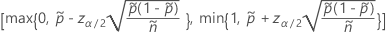
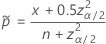
および
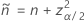
片側100(1 – α)%の下限には、次の式があります。
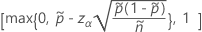
片側100(1 – α)%の上限には、次の式があります。
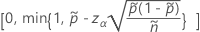
片側制限には、  の定義では、
の定義では、 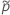 および
および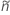 :
:
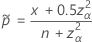
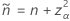
Agresti-Coull区間に対応する検定
分析では、信頼区間の手順を反転させることにより、検定のp値を計算します。
表記
| 用語 | 説明 |
|---|---|
| x | 事象数 |
| n | 試行回数 |
| zγ | γにおける標準正規分布の上側百分位点 |
| α | 1 – 信頼水準/100 |
Wald 正規近似の信頼区間
計算式

表記
| 用語 | 説明 |
|---|---|
 | 観測された確率、  = バツ / n = バツ / n |
| x | n回の試行における観測された事象数 |
| n | 試行回数 |
| Zα/2 | 1–α/2における標準正規分布の逆累積確率 |
| α | 1 – 信頼水準/100 |



