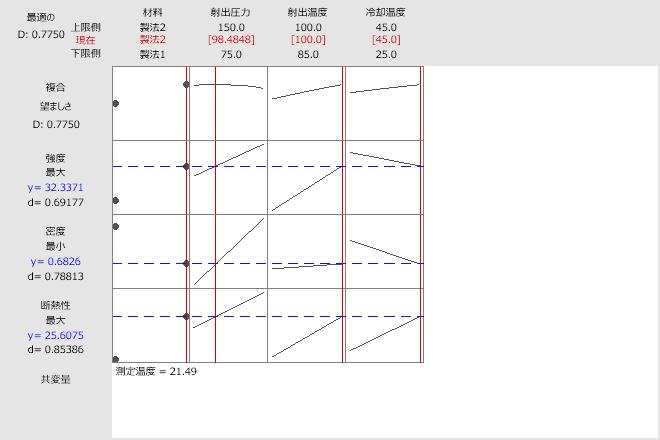
最適化プロット
最適化プロットでは、どの程度変数が予測応答に影響を与えるかを示します。最適化プロットをダブルクリックして対話モードに変更し、どの程度変数が予測応答に影響を与えるかを調べます。
最適化プロットが対話モードになると、セルには、対応する応答変数または複合的な望ましさが、その他のすべての変数が固定のままなのに対して、変数の1つの関数としてどの程度変化するかが表示されます。
- 各変数（予測変数）の列
- グラフに引かれた垂直な赤い線は、現在の設定を表しています。
- 各応答変数の行。
- 水平な青い線は、現在の応答値を表しています。
- 複合的な望ましさ
- 上の行と左上隅にあるのは、複合的な望ましさ（D）です。
- 対話用のツールバー
- 現在の変数設定の予測を計算するツールバーの左上にある「予測」ボタン。
Minitabが表示する適合値の種類は、モデル内の応答変数の種類によって変わります。たとえば、連続する測定値や度数などの測定値、2値データ、変動性の分析を使用するモデルがあるかどうかに合わせて、平均、確率、標準偏差が表示されます。
最適化プロットには予測変数設定の適合値が表示されます。ただし、予測区間を調べて、将来の値が1つ含まれる可能性がある値の範囲が、プロセスの許容範囲内に入っているかどうかを判断する必要があります。
解釈
最適化プロットを使用して、指定したパラメータを条件とする予測変数の最適な設定を決定します。
- 材料：この列の各セルにあたる2つの点は、カテゴリ変数の2つの水準、製法1と製法2を表しています。ここでは、製法2が最適材料であるように見えます。製法1に変更すると断熱度が下がり密度が上がってしまい、これはどちらも好ましくない変化です。ただし、材料は他の因子と交互作用があるため、この傾向は他の設定では見られないかもしれません。製法1の局所解が求められるかを検討してください。または、垂直バーを移動することで、グラフの製法1の設定値を直接変更することもできます。
- 射出圧力：射出圧力を増やすと3つの応答がすべて増加します。したがって、最適設定は因子水準範囲の中間にし（98.4848）、拮抗し合う各目的に対する妥協案とします。目標は、断熱度を最大化し、密度を最小化し、強度を最大にすることです。
- 射出温度：射出温度を上げると、応答がすべて増加します。しかし、密度に対する効果は、断熱度に対する効果に比べてごくわずかです。このため、複合的な望ましさは射出温度を最大化することにより高めることができます。射出温度の最適設定は、実験での最大水準であることがわかります。この結果から、より高い温度で実験を行うべきであるということが示されます。
- 冷却温度：冷却温度を上げると断熱度は増加しますが、密度と強度は減少します。射出温度と冷却温度の最適設定は、どちらも実験での最大水準になります。この結果から、より高い温度で実験を行うべきであるということが示されます。グラフからは、特に冷却温度を上げることは検討する価値があることがわかります。グラフの外挿が可能であれば、より高い冷却温度で断熱度と密度が改善される可能性もあります。ただし、強度は下がります。
パラメータ
Minitabでは、各応答についての計画パラメータがパラメータ表に表示されます。これらの結果を確認して、表示された計画パラメータが正しいかどうか検証する必要があります。
計画について到達点、下限、目標、上限、および重みを選択すると、各応答の満足関数が定義されます。重要度パラメータは、満足関数が単一の複合的な望ましさの値に統合される方法を決定します。
解釈
- 強度の到達点は、強度の最大化です。38.1821の値は優れていると見なされ、19.2189未満の値は不可と見なされます。
- 密度の到達点は、密度の最小化です。0.4351の値は優れていると見なされ、1.60314以上の値は不可と見なされます。
- 断熱度の到達点は、断熱度の最大化です。27.7156の値は優れていると見なされ、13.2905未満の値は不可と見なされます。
すべての3つの応答の重要度は同じ値です。したがって、すべての3つの応答の複合的な望ましさへの影響は等しいです。
複数応答予測
| 変数 | 設定 |
|---|---|
| 材料 | 製法2 |
| 射出圧力 | 98.4848 |
| 射出温度 | 100 |
| 冷却温度 | 45 |
| 測定温度 | 21.4875 |
| 応答 | 適合値 | 適合値の標準誤差 | 95%信頼区間 | 95%予測区間 |
|---|---|---|---|---|
| 強度 | 32.34 | 1.04 | (29.45, 35.22) | (27.25, 37.43) |
| 密度 | 0.6826 | 0.0597 | (0.5167, 0.8484) | (0.3899, 0.9753) |
| 断熱性 | 25.608 | 0.268 | (24.863, 26.352) | (24.294, 26.921) |
複数応答の予測
Minitabは、この表の変数設定を使用して、最適化手順に含まれる応答のすべての適合値を計算します。
まず応答の最適化機能を実行すると、複数応答の予測表は、アルゴリズムが特定する最適値を表示します。グラフの変数設定を変更し、ツールバーの予測するボタンをクリックする場合、Minitabは、この新しい設定でこの表を作成します。
この表を使って、目的の分析が行われたかどうかを検証してください。
適合値（Fit）
適合する値は、適合値または
. 適合値は、予測変数の値の平均応答の点推定です。予測変数の値は、X値とも呼ばれます。Minitabは回帰式と変数設定を使用して、適合値を計算します。
Minitabに表示される適合値の種類は、モデル内の応答変数の種類によって変わります。たとえば、Minitabには、連続測定値または計数測定値、2値データ、または変動性の分析を使用するモデルのどれがあるのかによって、平均、確率、または標準偏差が表示されます。
解釈
適合値は、X値を応答変数のモデル式に入力することで計算されます。
たとえば、式がy = 5 + 10xの場合に、X値が2ならば、適合値は25（25 = 5 + 10(2)）となります。
適合値の標準誤差（SE Fit）
適合値の標準誤差（SE Fit）は、特定の変数設定について推定される平均応答の変動を推定します。平均応答の信頼区間の計算には、適合値の標準誤差が使用されます。標準誤差は常に正数です。
解釈
適合値の標準誤差は、平均応答の推定値の精度を測定するために使用します。標準誤差が小さいほど、予測される平均応答の精度は高くなります。たとえば、分析者が配達時間を予測するモデルを開発するとします。変数設定のひとつのセットに、モデルは3.80日の平均配達時間を予測します。これらの設定の適合値の標準誤差は0.08日です。変数設定の2つめのセットに、モデルは適合値の標準誤差の0.02日で同じ平均配達時間を生成します。分析者は、変数設定の2つめのセットの平均配達時間が3.80日近くであるということに、より自信を持つことができます。
適合値とともに、適合値の標準誤差を使用して、平均応答の信頼区間を作成できます。たとえば、自由度の数に基づいて、95%の信頼区間は予測平均から標準誤差のおよそ2個分の範囲になっています。配達時間では、標準誤差が0.08日の際の予測平均の3.80日の95%の信頼区間は、（3.64、3.96）日です。これは、95%の信頼度で、母集団の平均がこの範囲に含まれることを意味します。標準誤差が0.02日の際、95%の信頼区間は、（3.76、3.84）日です。変数設定の２つめのセットの信頼区間は、標準誤差がより小さいことから、より狭くなります。
95%の信頼区間（CI）
適合値の信頼区間は、指定された予測を条件として、応答平均値になる可能性のある値の範囲を表します。
解釈
信頼区間を使用して、変数の観測値に関する適合値の推定値を評価します。
たとえば、信頼水準が95%の場合は、モデル内の指定された値の変数を持つ母集団平均が含まれる信頼区間を95%信頼できます。信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広い場合、将来価値の平均値に対する信頼性が低くなります。信頼区間が広すぎて役に立たない場合、サンプルのサイズを増加させることを検討します。
95%の予測区間（PI）
予測区間は、変数設定の選択された組み合わせの単一の将来の応答が含まれる可能性のある範囲です。
解釈
予測区間（PI）を使用して予測の精度を評価します。予測区間から、結果の実質的な有意性を評価できます。予測区間が許容範囲を超える場合は、予測は要求に対して十分に正確ではない可能性があります。
95%の予測区間の場合、95%の信頼度で、指定された予測を条件として、1つの応答が区間に含まれます。平均応答の場合と比較して、単一の応答を予測する際には不確実性が増加するので、予測区間は必ず信頼区間よりも広くなります。
たとえば、家具メーカーの材料技師は単回帰モデルを開発して、パーティクルボードの密度からそのボードの剛性を予測します。技師は、モデルが分析の仮定を満たすかどうかを検証します。その後、モデルを使用して、剛性を予測します。
回帰式では新しい観測値の剛性が、密度が25のとき-21.53 + 3.541*25、つまり66.995であることを予測します。こうした観測値の剛性値が厳密に66.995になる可能性は低いと考えられますが、予測区間は実際の値が95%の信頼度でおよそ48～86になるであろうことを示します。
複合的な望ましさ
複合的な望ましさ（D）を使用して、設定が一連の応答全体をどれだけ最適化するかを評価します。望特性の値の範囲は0～1です。1は理想的なケースを表し、0は、1つ以上の応答が許容限界の外にあることを表します。
多くの場合、応答が複数あると、すべての応答の望特性を同時に最大化する因子設定はありません。こうした理由から、Minitabは複合的な望ましさを最大化します。複合的な望ましさは、すべての応答変数に対する個別望特性を単一の測度にまとめたものです。その際、重要度の高い応答変数はより強調します。
詳細は個別の望ましさと複合的な望ましさとはを参照してください。
解釈
複合的な望ましさの値は1に非常に近く、この設定によってすべての応答の望ましい結果を達成できることを示しています。
