金融アナリストが、大学の生徒が特定のクレジットカードを保有している確率に関連する因子を調査しているとします。アナリストは、アンケートから大学の生徒の標本を無作為に作成します。アンケートでは、教育や経済状況に関する質問を生徒にしました。
アナリストは、マーケティングを目的として、MasterCardのクレジットカードを所持する可能性は低いものの、American Expressカードを所持する可能性が高い生徒の母集団と関連性のある予測値を特定したいと思っています。アナリストは、American ExpressとMasterCardの両方に2値ロジスティック回帰モデルを適合して、予測変数とそれぞれのクレジットカードを保有する確率の関連性を判定します。
モデル適合後、技師は、応答の最適化機能を使用して、両方のクレジットカードの確率を許容可能にする予測変数設定を見つけます。
- 標本データを開く、 クレジット調査.MWX.
- を選択します。
- MasterCardの行の目的で最小化を選択します。
- American Expressの行の目的で最大化を選択します。
- OKをクリックします。
結果を解釈する
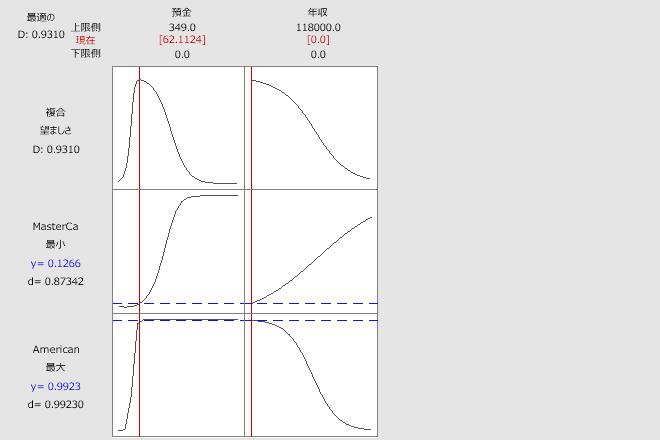
Minitabは、2つの保存モデルを使用して、両方の応答変数の値を最適化する予測変数設定を推定します。これらの2つの応答を組み合わせた望ましさ(「複合的な望ましさ」とも呼ばれます)は0.9310であり、優れた解であることを示していますが、完璧な解ではありません。
グラフで示される予測変数設定は、MasterCardのクレジットカードを所持する可能性が低いものの、American Expressカードを所持する可能性が高い生徒と関連付けられます。この生徒の母集団の平均は、62.11ドルの現金とゼロの年収です。この出力は、これらの値の適合可能性が、Master Cardでは0.127、American Expressでは0.9923であることを示しています。信頼区間は、これらの予測の精度を示します。
プロット上でこの初期解の変数設定を直接調整することができます。縦のバーを移動して因子設定を変更し、応答の個別望特性(d)と複合的な望ましさがどのように変化するかを見ます。
パラメータ
| 応答 | 目的 | 下限 | 目標値 | 上限 | 重み | 重要度 |
|---|---|---|---|---|---|---|
| MasterCard | 最小 | 0 | 1 | 1 | 1 | |
| American Express | 最大 | 0 | 1 | 1 | 1 |
解決方法
| 解決方法 | 預金 | 年収 | MasterCard 適合確率 | American Express 適合確率 | 複合的望ましさ |
|---|---|---|---|---|---|
| 1 | 62.1124 | 0 | 0.126577 | 0.992297 | 0.930964 |
複数応答予測
| 変数 | 設定 |
|---|---|
| 預金 | 62.1124 |
| 年収 | 0 |
| 応答 | 適合確率 | 適合値の標準誤差 | 95%信頼区間 |
|---|---|---|---|
| MasterCard | 0.127 | 0.172 | (0.007, 0.754) |
| American Express | 0.9923 | 0.0322 | (0.0323, 1.0000) |
