回帰式
回帰式を使用して、モデルにおける応答と項の関係を表します。回帰式は回帰線の代数で表現されます。線形モデルの回帰式は次の形式を取ります。Y = b0 + b1x1回帰式では、Yが応答変数、b0が定数または切片、b1が線形項の推定係数（線の傾き）、x1が項の値を表します。
2つ以上の項を持つ回帰式は、次の形式を取ります。
y = b0 + b1X1 + b2X2 + ...+ bkXk
- yは応答変数
- b0 は定数です
- b1、b2、...、bk は係数です
- X1、X2、...、Xk は項の値です。各項は1つの予測変数、多項式の項、または交互作用項になり得ます。
Minitabは式と変数設定を使用して、適合値を計算します。
変数設定
Minitabは回帰式と変数設定を使用して、適合値を計算します。変数設定が、モデルの推定に使用するデータと比較して異常な場合、予測の下に警告が表示されます。
変数設定表を使い、目的の分析が行われたかどうかを検証してください。
適合値（Fit）
適合する値は、適合値または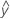
. 適合値は、予測変数の値の平均応答の点推定です。予測変数の値は、X値とも呼ばれます。Minitabは回帰式と変数設定を使用して、適合値を計算します。
Minitabに表示される適合値の種類は、モデル内の応答変数の種類によって変わります。たとえば、Minitabには、連続測定値または計数測定値、2値データ、または変動性の分析を使用するモデルのどれがあるのかによって、平均、確率、または標準偏差が表示されます。
解釈
適合値は、X値を応答変数のモデル式に入力することで計算されます。
たとえば、式がy = 5 + 10xの場合に、X値が2ならば、適合値は25（25 = 5 + 10(2)）となります。
適合値の標準誤差（SE Fit）
適合値の標準誤差（SE Fit）は、特定の変数設定について推定される平均応答の変動を推定します。平均応答の信頼区間の計算には、適合値の標準誤差が使用されます。標準誤差は常に正数です。この解析では、 統計 メニューのモデルと 予測分析モジュールの 線形回帰 モデルと 2値ロジスティック回帰 モデルの標準誤差が計算されます。
解釈
適合値の標準誤差は、平均応答の推定値の精度を測定するために使用します。標準誤差が小さいほど、予測される平均応答の精度は高くなります。たとえば、分析者が配達時間を予測するモデルを開発するとします。変数設定のひとつのセットに、モデルは3.80日の平均配達時間を予測します。これらの設定の適合値の標準誤差は0.08日です。変数設定の2つめのセットに、モデルは適合値の標準誤差の0.02日で同じ平均配達時間を生成します。分析者は、変数設定の2つめのセットの平均配達時間が3.80日近くであるということに、より自信を持つことができます。
あてはめ値を使用すると、近似の標準誤差を使用して、平均応答の信頼区間を作成できます。たとえば、自由度の数に応じて、95% 信頼区間は、予測平均の上下に約 2 つの標準誤差を拡張します。配達時間の場合、標準誤差が 0.08 の場合の予測平均 3.80 日の 95% 信頼区間は (3.64, 3.96) 日です。これは、95%の信頼度で、母集団の平均がこの範囲に含まれることを意味します。標準誤差が 0.02 の場合、95% 信頼区間は (3.76, 3.84) 日です。変数設定の 2 番目のセットの信頼区間は、標準誤差が小さいため、より狭くなります。
95%信頼区間
近似の信頼区間は、予測変数の指定された設定が与えられた場合の平均応答の可能値の範囲を提供します。この分析では、 統計 メニューのモデルと、 予測分析モジュールの 線形回帰 と 2値ロジスティック回帰 のモデルの信頼区間が計算されます。
解釈
信頼区間を使用して、変数の観測値の適合値の推定値を評価します。
たとえば、95% の信頼水準では、信頼区間にモデル内の変数の指定された値の母平均が含まれていると 95% の信頼度を持つことができます。信頼区間は、結果の実際的な重要性を評価するのに役立ちます。専門知識を活用して、信頼区間に状況にとって実際的に重要な値が含まれているかどうかを判断します。信頼区間が広いということは、将来の値の平均について信頼が低くなる可能性があることを示します。信頼区間が広すぎて役に立たない場合、サンプルサイズを増加させることを検討します。
95%予測区間
予測区間は、選択した変数設定の組み合わせに対する単一の将来の応答を含む可能性が高い範囲です。この分析では、 統計 メニューのモデルと 予測分析モジュールの 線形回帰 モデルの予測区間が計算されます。
解釈
予測間隔 (PI) を使用して、予測の精度を評価します。予測区間から、結果の実質的な有意性を評価できます。 予測間隔が許容範囲外に広がると、予測が要件に対して十分に正確ではない可能性があります。
95% の PI では、指定した予測変数の設定が与えられた場合、1 つの応答が区間に含まれると 95% の確信を得ることができます。予測区間は、単一の応答と平均応答の予測に伴う不確実性が加わるため、常に信頼区間よりも広くなります。
たとえば、家具メーカーの材料エンジニアが、基板の密度からパーティクルボードの剛性を予測する単純な回帰モデルを開発します。エンジニアは、モデルが分析の仮定を満たすかどうかを検証します。次に、アナリストはモデルを使用して剛性を予測します。
たとえば、回帰式は、新しい観測値に対して予測される剛性が、密度が25のとき-21.53 + 3.541*25、つまり66.995であることを予測します。このような観測値の剛性が正確に 66.995 になる可能性は低いですが、予測区間は、エンジニアが実際の値が約 48 から 86 の間になると 95% 確信できることを示しています。
