多重ペアワイズ比較におけるグループ化情報表
Minitabは、2つの水準平均の差に対する信頼区間の結果を用いてグループ化情報を求めます。グループ化情報は行列で示されます。項がk個の水準を持つと仮定すると、行列は最大k×kとなります。全ての水準が1つのグループに入っている場合は、次元はk×kとなり、全ての因子水準に文字Aが与えられます。全ての水準が別々のグループに入っている場合は、k×kとなり対角線のみ文字が与えられます。
- 項のさまざまな水準の最小二乗平均を降順で並べ替え、1, 2, ... , kとして表します。
- 全てのセルに0を設定しk×kの行列を定義します。k=因子水準の数です。
- Minitabではj=1, ... となるj列には以下の処理を行います。
- 平均j - 平均r(r=j+1 .. , k)の信頼区間を判定します。rの区間に0が含まれる場合、r番目の行とj番目の列のセルjに1を設定します。
- j列に1つでも値1がある場合はセル(j, j)に1を設定します。
- 行I = j + 1, ... , kに対し、1からjまでの列の合計を計算します。最小値(全行の合計)>= 1の場合、ループを終了するか、jに1を加算しステップaに移行します。
- Minitabは、i行の全てに対し、列の合計値が≥ 1かどうかを判定します。合計値が0の場合、i行j列のセルを1に設定し、ここでj列は行列のなかで初めて0値をもっていることになる。(j列でその合計値が行列の中で最初の0である場合、セルi行j列=1と設定します。)この手法により1と0の行列が生成され、グループの総数は0ではない列の数となります。
- Minitabは列に文字を割り当て(例:列1にA、列2にBなど)、値が1となっているセルに対して正しい文字を割り付けます。
対照との多重比較におけるグループ化情報表
Minitabは、各水準平均と対照水準の差に対する信頼区間の結果を用いてグループ化情報を求めます。グループ化情報は1列の行列で示されます。
Minitabは対照水準に対して文字「A」を割り当てます。
区間に0が含まれる場合は、水準平均が対照水準と同じグループに入っていることになります。Minitabは水準平均に対して文字「A」を割り当てます。
区間に0が含まれない場合は、文字は割り当てられません。
テューキーの方法
計算式
テューキーの方法はすべてのペアワイズ比較に利用できます。信頼区間の計算式は以下になります。
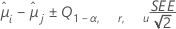
検定統計量の計算式は以下になります。

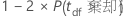
調整されたp値の計算に関する詳細は下記の参考文献を参照してください。
同時過誤率から個別過誤率を抽出するには以下の計算式を使用します。
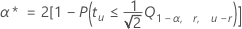
表記
| 用語 | 説明 |
|---|---|
 | i番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
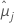 | j番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
| r | 平均の数 |
| Q1 − α, r, u | u自由度と比較する、r平均のスチューデント化された範囲分布の1 − α百分位 |
| u | モデルから得られる誤差の自由度 |
| SEE | 最小二乗平均間の推定された差の標準誤差 |
| α | 第一種過誤が発生する同時確率(スチューデント化された範囲分布に基づく) |
| α* | 第1種過誤が発生する個別確率(1回の比較のt分布に基づく) |
参考文献
1 Braun, H. I.編(1994年)、『The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983』、ニューヨーク: Chapman and Hall
2 J.C. Hsu(1996)、『Multiple Comparisons: Theory and methods』、Chapman & Hall
フィッシャーの方法
計算式
Minitabは、処理平均を比較するためのさまざまな信頼区間法を提供します。フィッシャーの方法では、信頼区間のエンドポイントとp値は、比較がペアワイズ比較であろうと、対照との比較であろうと同じです。フィッシャーの方法では、個別信頼水準を使用します。信頼区間の計算式は以下になります。
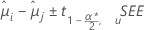
検定統計量の計算式は以下になります。

p値 = 2*P{ T u > tu}
個別過誤率から同時信頼水準を抽出するには以下の計算式を使用します。
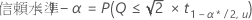
表記
| 用語 | 説明 |
|---|---|
 | i番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
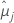 | j番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
| t1-α*/2, u | u自由度を持つスチューデント化t分布の上側α' /2百分位 |
| Tu | 誤差のu自由度を持つt分布を持つランダム変数 |
| Q | スチューデント化された範囲分布を持つランダム変数 |
| α | 第1種の過誤を発生する同時確率 |
| α* | 第1種の過誤を発生する個別確率 |
| u | モデルから得られる誤差の自由度 |
| SEE | 最小二乗平均間の推定された差の標準誤差 |
ボンフェローニ法
計算式
Minitabは、処理平均を比較するためのさまざまな信頼区間法を提供します。ボンフェローニ法では、比較間の依存性に関して仮説を立てないので、最も保守的な方法といえます。この文脈での「保守的」は、本当の信頼区間は、表示されている信頼区間よりも大きい可能性があることを意味します。信頼区間の計算式は以下になります。
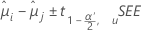
検定統計量の計算式は以下になります。

表記
| 用語 | 説明 |
|---|---|
 | i番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
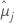 | j番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
| t1-α*/2, u | u自由度を持つスチューデント化t分布の上側α' /2百分位 |
| α | 第1種の過誤を発生する同時確率 |
| α' | α / c |
| c | 比較数 |
| u | モデルから得られる誤差の自由度 |
| SEE | 最小二乗平均間の推定された差の標準誤差 |
比較数は、ペアワイズ比較なのか、対照との比較なのかによって変わります。kが比較されている平均の数だとします。比較の数は以下の表にあります。
| ペアワイズ | k (k – 1) / 2 |
| 対照 | k – 1 |
シダックの方法
計算式
Minitabは、処理平均を比較するためのさまざまな信頼区間法を提供します。シダック法は、それぞれの比較が独立しているかのように比較を処理し、それにより真の過誤率の保守的な近似値を算出します。シダック法は、ボンフェローニ法よりも少しだけ効果的だと言えます。
信頼区間の計算式は以下になります。
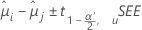
検定統計量の計算式は以下になります。

調整済みp値 = 1 − (1 − p)c
表記
| 用語 | 説明 |
|---|---|
 | i番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
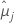 | j番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
| t1-α*/2, u | u自由度を持つスチューデント化t分布の上側α' /2百分位 |
| α | 第1種の過誤を発生する同時確率 |
| α' | 1 – (1 – α ) 1/ k |
| u | モデルから得られる誤差の自由度 |
| SEE | 最小二乗平均間の推定された差の標準誤差 |
| p | 比較のt分布から得られる調整されていないp値 |
| c | 比較数 |
比較数は、ペアワイズ比較であるか、対照との比較であるかによって変わります。kが因子の組み合わせ数であるとします。比較数は以下の表に記載されています。
| ペアワイズ | k (k – 1) / 2 |
| 対照 | k – 1 |
ダネットの方法
計算式
Minitabは、処理平均を比較するためのさまざまな信頼区間法を提供します。ダネットの方法は対照との比較に利用できます。信頼区間の計算式は以下になります。

検定統計量の計算式は以下になります。

調整済みp値は、ダネットが検定統計量に提案する分布を積分した結果です。詳細は下記の参考文献を参照してください。
表記
| 用語 | 説明 |
|---|---|
 | i番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
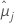 | j番目の要因計画または要因計画水準の組み合わせの最小二乗平均 |
| D1-α, k-1, u | k − 1比較とu自由度を持つダネット法が提案する上側α百分位 |
| α | 第1種の過誤を発生する同時確率 |
| k | 比較する平均の個数 |
| u | モデルから得られる誤差の自由度 |
| SEE | 最小二乗平均間の推定された差の標準誤差 |
参考文献
1 Dunnett, C. W.(1955年1月1日)、「A multiple comparison procedure for comparing several treatments with a control」『Journal of the American Statistical Association』第50巻、1096-1121頁
2 J.C. Hsu(1996年)、『Multiple Comparisons: Theory and methods』、Chapman & Hall
