時系列を分析するための手法

単純な予測と平滑化の方法では、通常はデータの時系列プロットで容易に観測される系列内の成分をモデル化します。この方法では、データをその成分部に分解してから、それらの成分の推定値を拡張して将来の予測値を求めます。静的方法（トレンド分析および分解）を選択するか、動的方法（移動平均法、1系列指数平滑化と二重指数平滑化、およびWinterの方法）を選択することがができます。静的方法には時間の経過に伴って変化しないパターンがあり、動的方法には、時間の経過に伴って変化するパターンがあって、隣接する値を使用して推定値が更新されます。

これら2つの方法を組み合わせて使用することもできます。つまり、1つの静的方法を選択して1つの成分をモデル化し、1つの動的方法を選択して別の成分をモデル化することができます。たとえば、トレンド分析を使用して静的なトレンドを当てはめ、Winterの方法を使用して残差の季節成分を動的にモデル化することができます。あるいは、分解を使用して静的季節モデルを当てはめ、二重指数平滑化を使用して残差のトレンド成分を動的にモデル化することもできます。また、トレンド分析と分解を同時に適用し、トレンド分析によって得られるさまざまなトレンドモデルを使用できるようにすることができます。いくつかの方法を組み合わせて使用する場合の欠点は、予測の信頼区間が有効ではなくなることです。

それぞれの方法について、共通データの適合値と予測値の要約およびグラフを示した表を以下に示します。

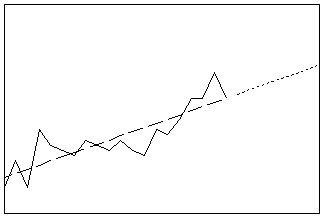
トレンド分析

一般的なトレンドモデルを時系列データに当てはめます。線形モデル、2次モデル、指数的増加または減衰モデル、S曲線トレンドモデルの中から選択します。この方法を使用してトレンドを当てはめるのは、系列に季節成分がない場合です。

予測:

• 長さ: 長期
• プロファイル: トレンド線の延長

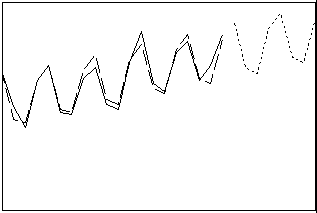
分解

時系列を、線形トレンド成分、季節成分、および誤差に分離します。季節成分が、トレンドとの関係で加法的か、または乗法的かを選択します。この方法を使用して予測を行うのは、系列に季節成分が含まれる場合か、または各成分の性質を調べる場合です。

予測:

• 長さ: 長期
• プロファイル: 季節パターンのあるトレンド

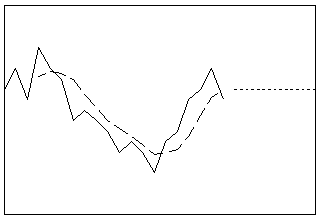
移動平均

系列内の連続する観測値の平均を求めることによってデータを平滑化します。この方法は、データにトレンド成分がない場合に使用できます。季節成分がある場合は、移動平均の長さを季節サイクルの長さと等しい長さに設定します。

予測:

• 長さ: 短期
• プロファイル: 直線

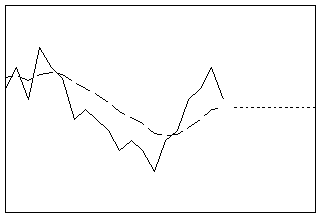
1系列指数平滑化

最適な1ステップ先のARIMA (0,1,1)予測計算式を使用してデータを平滑化します。この方法は、トレンド成分または季節成分が存在しない場合に最も有効です。移動平均モデルにおける単一の動的成分は水準です。

予測:

• 長さ: 短期
• プロファイル: 直線

二重指数平滑化

最適な1ステップ先のARIMA (0,2,2)予測計算式を使用してデータを平滑化します。この方法は、トレンドがあっても、一般的な平滑化法としても使用可能な場合に有効です。二重指数平滑化では、水準とトレンドという2つの成分の動的推定値を計算します。

予測:

• 長さ: 短期
• プロファイル: 最後のトレンド推定値と傾きが等しい直線

Winterの方法

Holt-Winter指数平滑化によってデータを平滑化します。この方法を使用するのは、トレンドと季節性があり、それら2つの成分が加法的または乗法的である場合です。Winterの方法では、水準、トレンド、季節という3つの成分の動的推定値を計算します。

予測:

• 長さ: 短期から中期
• プロファイル: 季節パターンのあるトレンド

ARIMA（自己回帰和分移動平均）モデリングでも、データ内のパターンを利用しますが、これらのパターンはデータのプロットで容易に視覚化できない可能性があります。そのため、ARIMAモデリングでは、代わりに階差、自己相関関数、および偏自己相関関数を使用して、許容可能なモデルを特定することができるようにしています。

ARIMAモデリングを使用して、トレンド成分と季節成分があるかどうかに関係なく、多種多様な時系列をモデル化して予測を行うことができます。予測プロファイルは、当てはめるモデルに依存します。単純な予測と平滑化の方法と比較した場合のARIMAモデリングの利点は、データを当てはめる場合の柔軟性が高まることです。ただし、モデルを識別して当てはめる処理には時間がかかる可能性があり、ARIMAモデリングの自動化は容易ではありません。

階差

時系列のデータ値間の階差を計算して保存します。ARIMAモデルを当てはめたくても、データにトレンド成分や季節成分がある場合は、データの階差を取ることが、適合性の高いARIMAモデルを評価する際の一般的なステップです。　

遅れ

時系列の遅れを計算して保存します。時系列を遅らせると、Minitabによって元の値が列の下方に移動され、列の最上部に欠損値が挿入されます。挿入される欠損値の数は、遅れの長さに依存します。

自己相関

時系列の自己相関を計算してグラフを作成します。自己相関は、k時間単位離れた時系列の観測値間の相関です。自己相関のプロットは、自己相関関数（ACF）と呼ばれます。ACFを表示し、それに基づいてARIMAモデルに含める項を選択することができます。

偏自己相関

時系列の偏自己相関を計算してグラフを作成します。偏自己相関は、自己相関と同様、時系列の順序付けされたデータペアのセットどうしの相関です。回帰モデルでの偏相関の場合と同様、偏自己相関では、説明対象のその他の項との関係の強度を測定します。遅れkでの偏自己相関は、自己回帰モデルの時間tでの残差と、自己回帰モデルのすべての介入遅れの項を含む遅れkでの観測値の間の相関です。偏自己相関のプロットは、偏自己相関関数（PACF）と呼ばれます。PACFの表示に基づいて、ARIMAモデルに含める項を選択することができます。

相互相関

2つの時系列間の相関を計算してグラフを作成します。

ARIMA

Box-Jenkins ARIMAモデルを時系列に当てはめます。ARIMAにおいて、「自己回帰」、「和分」、および「移動平均」は、ランダム雑音のみが残されるまでARIMAモデルを計算する際に行われるフィルタリングステップを指します。ARIMAを使用して、時系列の動向をモデル化し、予測を行います。