Winterの方法の方法と計算式

乗法

計算式

乗法モデル:

L_t = α (Y_t / S_t–p) + (1 – α) [L_t–1 + T_t–1]
T_t = γ [L_t – L_t–1] + (1 – γ) T_t–1
S_t = δ (Y_t / L_t) + (1 – δ) S_t–p
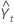= (L_t–1 + T_t–1) S_t–p

表記

用語	説明
L_t	時間tでの水準、αはその水準の重み
T_t	時間tでのトレンド、
γ	トレンドの重み
S_t	時間tでの季別成分
δ	季節成分の重み
p	季節期間
Y_t	時間tでのデータ値
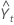	時間tでの適合値、または1期間先の予測

乗法モデルで水準とトレンドの初期値を計算する方法

次の方法では、季節長が4より大きいと仮定します。

データの平均値、最小値、最大値を見つけます。例:
- 平均 = 554.208
- 最小 = 1
- 最大 = 1498.47
データの各行について、次の計算を行います。
Nは季節長に等しくします。この例では、 N = 12にします。
最初のN個のtemp値(ステップ2で計算済み)をY変数として、ベクトル1からNをX変数として使用して回帰を実行します。例:
Y X

4104.36 1

4104.36 2

4630.36 3

4922.80 4

4822.40 5

5601.83 6

4891.77 7

4604.44 8

4411.26 9

4123.66 10

4104.36 11

4104.36 12

回帰直線の傾きはトレンドの初期値です。
次の値を引いて回帰直線の切片を調整します：

Y	X
4104.36	1
4104.36	2
4630.36	3
4922.80	4
4822.40	5
5601.83	6
4891.77	7
4604.44	8
4411.26	9
4123.66	10
4104.36	11
4104.36	12

データに対する切片は4705.24です。切片から4103.36を引き、調整された切片601.879を取得します。この調整済み切片は、水準の初期値です。

加法

計算式

加法的モデルの場合:

L_t = α (Y_t – S_t–p) + (1 – α) [L_t–1 + T_t–1]
T_t = γ [L_t – L_t–1] + (1 – γ) T_t–1
S_t = δ (Y_t – L_t) + (1 – δ) S_t–p
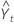= L_t–1 + T_t–1 + S_t–p

表記

用語	説明
L_t	時間tでの水準、αはその水準の重み
T_t	時間tでのトレンド、
γ	トレンドの重み
S_t	時間tでの季別成分
δ	季節成分の重み
p	季節期間
Y_t	時間tでのデータ値
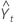	時間tでの適合値、または1期間先の予測

加法的モデルで水準とトレンドの初期値を計算する方法

次の方法では、季節長が4より大きいと仮定します。

Nは季節長に等しくします。この例では、 N = 12にします。
最初のN個のデータ値をY変数として、ベクトル1からNをX変数として使用して回帰を実行します。例:
Y X

1.00 1

1.00 2

527.00 3

819.45 4

719.04 5

1498.47 6

788.42 7

501.08 8

307.90 9

20.30 10

1.00 11

1.00 12

回帰直線の傾きはトレンドの初期値です。回帰直線の切片は水準の初期値です。

加法モデルで季節指標の初期値を計算する方法

次の方法では、季節長が4より大きいと仮定します。

データ値をY変数として、ベクトル1から24をX変数として使用して回帰を実行します。例:

Y	X
1.00	1
1.00	2
527.00	3
819.45	4
719.04	5
1498.47	6
788.42	7
501.08	8
307.90	9
20.30	10
1.00	11
1.00	12
83.00	13
668.21	14
1121.28	15
1386.84	16
1031.18	17
988.60	18
1380.30	19
1005.97	20
233.69	21
211.87	22
2.00	23
2.40	24

この回帰モデルの残差を次の手順で使用します。

残差をY変数として、12個の指標変数(z.1 ～ z.12)をX変数として使用して回帰を実行します。切片(定数)項を使用せずに回帰モデルを適合させます。例:

残差	z.1	z.2	z.3	z.4	z.5	z.6	z.7	z.8	z.9	z.10	z.11	z.12
-508.261	1	0	0	0	0	0	0	0	0	0	0	0
-512.170	0	1	0	0	0	0	0	0	0	0	0	0
9.926	0	0	1	0	0	0	0	0	0	0	0	0
298.460	0	0	0	1	0	0	0	0	0	0	0	0
194.145	0	0	0	0	1	0	0	0	0	0	0	0
969.667	0	0	0	0	0	1	0	0	0	0	0	0
255.705	0	0	0	0	0	0	1	0	0	0	0	0
-35.538	0	0	0	0	0	0	0	1	0	0	0	0
-232.625	0	0	0	0	0	0	0	0	1	0	0	0
-524.137	0	0	0	0	0	0	0	0	0	1	0	0
-547.346	0	0	0	0	0	0	0	0	0	0	1	0
-551.254	0	0	0	0	0	0	0	0	0	0	0	1
-473.161	1	0	0	0	0	0	0	0	0	0	0	0
108.141	0	1	0	0	0	0	0	0	0	0	0	0
557.303	0	0	1	0	0	0	0	0	0	0	0	0
818.952	0	0	0	1	0	0	0	0	0	0	0	0
459.378	0	0	0	0	1	0	0	0	0	0	0	0
412.890	0	0	0	0	0	1	0	0	0	0	0	0
800.684	0	0	0	0	0	0	1	0	0	0	0	0
422.451	0	0	0	0	0	0	0	1	0	0	0	0
-353.739	0	0	0	0	0	0	0	0	1	0	0	0
-379.468	0	0	0	0	0	0	0	0	0	1	0	0
-593.247	0	0	0	0	0	0	0	0	0	0	1	0

この回帰モデルの係数は、季節指数の初期値です。係数は次のとおりです。

時期	COEF1
1	-490.711
2	-202.014
3	283.615
4	558.706
5	326.762
6	691.278
7	528.195
8	193.456
9	-293.182
10	-451.803
11	-570.297
12	-574.005

注

指標変数 z.1 ～ z.12 は、各データポイントが属する期間の月を示します。たとえば、変数 z.1 は期間の最初の月の1と等しく、それ以外の場合は0に等しくなります。

モデルの当てはめ

Winterの方法では、各期間で1つの水準成分、1つのトレンド成分、および1つの季節成分を使用します。3つの重み値（平滑化パラメータ）を使用して、各期間で成分を更新します。水準成分とトレンド成分の初期値は、その時点で線形回帰から得られます。季節成分の初期値は、トレンド除去データを使用するダミー変数回帰から得られます。

予測

Winterの方法では、水準成分、トレンド成分、および季節成分を使用して予測を行います。また、Winterの方法では、予測原点時刻までのデータを使用した予測も行います。

計算式

時間tの点からm期間先の予測:

乗法的方法: (L_t + mT_t) * S_t + m −p
加法的方法: L_t + mT_t +S_t + m −p

表記

用語	説明
L_t	水準
T_t	時間tでのトレンド

用語	説明
S_t + m −p	前年の同じ期間の季節成分

MAPE

平均絶対パーセント誤差（MAPE）により、当てはめられた時系列値の精度を測定します。MAPEでは、精度をパーセントで表します。

計算式

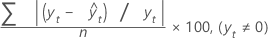
表記

用語	説明
y_t	時間tでの実際の値
	適合値
n	観測値数

MAD

平均絶対偏差（MAD）により、適合された時系列の値の精度を測定します。MADでは、精度がデータと同じ単位で表されるため、誤差の量を概念化するのに役立ちます。

計算式

表記

用語	説明
y_t	時間tでの実際の値
	適合値
n	観測値数

MSD

平方平均偏差（MSD）は、モデルに関係なく、必ず同じ分母nを使用して計算されます。MSDは、MADよりも高感度な、異常に大きな予測誤差の測度です。

計算式

表記

用語	説明
y_t	時間tでの実際の値
	適合値
n	観測値数

Winterの方法の方法と計算式

このトピックの内容

乗法

計算式

表記

乗法モデルで水準とトレンドの初期値を計算する方法

加法

計算式

表記

加法的モデルで水準とトレンドの初期値を計算する方法

加法モデルで季節指標の初期値を計算する方法

注

モデルの当てはめ

予測

計算式

表記

MAPE

計算式

表記

MAD

計算式

表記

MSD

計算式

表記