偏自己相関関数は、遅れが短いその他のすべての項(yt-1、yt-2、...、yt-k-1)の存在を考慮して調整した後に計算される、k時間単位離れた時系列の観測値間の相関(ytとyt-k)を表す測度です。
解釈
偏自己相関関数と自己相関関数を併用して、ARIMAモデルを特定します。偏自己相関関数で以下のパターンを探します。各遅れでのスパイクを調べ、それらのスパイクが有意かどうか判断します。有意なスパイクは有意限界を越えて広がっており、これは、その遅れの相関がゼロにならないことを示します。
| パターン | 考えられる要因 | 例 |
|---|---|---|
| 少数の遅れの後に減少する遅れ1での大きなスパイク。 | データの移動平均項。偏自己相関関数を使用して、移動平均項の次数を判断します。 | 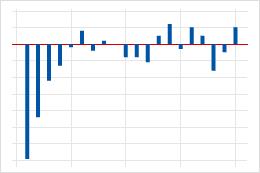 |
| その後に正と負の相関を交互に示す減衰波が続く、遅れ1での大きなスパイク。 | データの次数の高い移動平均項。自己相関関数を使用して、移動平均項の次数を判断します。 | 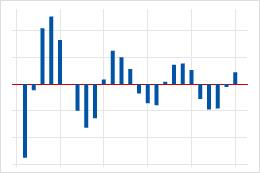 |
| その後に有意ではない相関が続く、最初または2番目の遅れでの有意相関。 | データに含まれる自己回帰項。有意相関の数は、自己回帰項の次数を示します。 | 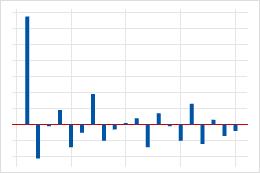 |
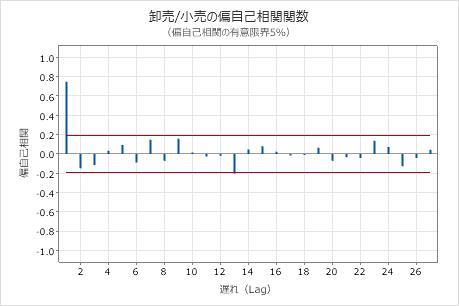
このプロットでは、遅れ1で有意相関があり、その後に有意ではない相関が続いています。このパターンは、次数が1の自己回帰を示します。
