移動平均の方法と計算式

移動平均を計算するため、Minitabでは、系列での観測値の連続するグループの平均を求めます。たとえば、系列が4、5、8、9、10の数値で始まり、移動平均の長さを3にするとします。このとき、移動平均の最初の2つの数値は欠損します。移動平均の3番目の値は4、5、8の平均、4番目の値は5、8、9の平均、5番目の値は8、9、10の平均です。

デフォルトでは、移動平均値は計算が行われた期間に配置されます。たとえば、長さ3の移動平均の場合には、最初の移動平均の数値は期間3に配置され、次の移動平均は期間4に配置されます（以降はその繰り返し）。

移動平均を中心化すると、範囲の最後ではなく、範囲の中央に配置されます。これは、移動平均値を時間的な中心に配置するためです。

移動平均の長さが奇数の場合

移動平均の長さが3であるとします。この場合Minitabでは、最初の数値移動平均値が期間2に配置され、次の移動平均値は期間3に配置され、以下同様に配置されます。この場合、最初の期間と最後の期間の移動平均値は欠損値（*）になります。

移動平均の長さが偶数の場合

移動平均の長さが4であるとします。この場合、移動平均値を期間2.5に配置することはできないため、Minitabでは、最初の4つの値の平均値を計算し、その値をMA1と命名します。次にMinitabでは、次の4つの値の平均値を計算して、MA2と命名します。それら2つの値の平均が、Minitabで期間3に配置される数値となります。この場合、最初の2つと最後の2つの期間の移動平均値は欠損値（*）になります。

時間tでの適合値は、時間t-1での中心化されていない移動平均値です。10時間単位先を予測する場合、各時間の予測値は原点での適合値になります。移動平均の計算には、原点までのデータが使用されます。

線形移動平均法は、連続する移動平均を計算することによって使用できます。線形移動平均法は、多くの場合、データにトレンドがない場合に使用されます。まず、元の系列の移動平均を計算して保存します。次に、保存済みの列の移動平均を計算して保存し、2番目の移動平均を求めます。

単純な予測において、時間tの予測値は時間t - 1でのデータ値です。長さが1の移動平均を使用する移動平均法を実行することにより、単純な予測を行うことができます。

計算式

上限 = 予測値 + 1.96 ×

下限 = 予測値 – 1.96 ×

表記

平均絶対パーセント誤差（MAPE）により、当てはめられた時系列値の精度を測定します。MAPEでは、精度をパーセントで表します。

計算式

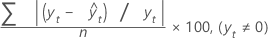
表記

用語	説明
yt	時間tでの実際の値
	適合値
n	観測値数

平均絶対偏差（MAD）により、適合された時系列の値の精度を測定します。MADでは、精度がデータと同じ単位で表されるため、誤差の量を概念化するのに役立ちます。

計算式

表記

用語	説明
yt	時間tでの実際の値
	適合値
n	観測値数

平方平均偏差（MSD）は、モデルに関係なく、必ず同じ分母nを使用して計算されます。MSDは、MADよりも高感度な、異常に大きな予測誤差の測度です。

計算式

表記

用語	説明
yt	時間tでの実際の値
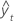	適合値
n	観測値数