の主要な結果を解釈するベスト ARIMA モデルによる予測

以下のステップを実行して、モデル選択プロセスと ARIMA 分析の結果を解釈します。主要な出力には、モデル選択統計量、p値、係数、リュングボックスカイ二乗統計量、残差の自己相関関数が含まれます。

このトピックの内容

ステップ1：代替モデルを検討する
ステップ 2: モデル内の各項が有意かどうかを判断する
ステップ3：モデルが分析の仮定を満たすかどうか判断する

ステップ1：代替モデルを検討する

「モデル選択」(Model Selection Table) テーブルには、検索内の各モデルの基準が表示されます。この表には、p が自己回帰項、d が差分項、q が移動平均項である項の順序が表示されます。季節用語は大文字を使用し、非季節用語は小文字を使用します。

異なるモデルを比較する際はAIC、AICc、BICを使用します。小さい値が好ましいと考えられます。ただし、項のセットの値が最も小さいモデルは、必ずしもデータにうまく適合するとは限りません。検定とプロットを使用して、モデルがデータにどの程度適合するかを評価します。デフォルトでは、ARIMA の結果は AICc の最適値を持つモデルに対するものです。

選択すると、「モデル選択代替モデルの選択」(Model Selection Table) を含むダイアログが開きます。基準を比較して、同様のパフォーマンスを持つモデルを調査します。

ARIMA出力を使用して、モデル内の項が統計的に有意であり、モデルが分析の仮定を満たしていることを確認します。表内のどのモデルもデータにうまく適合しない場合は、差分順序が異なるモデルを検討します。

また、代替モデルが最適モデルとほぼ同じパフォーマンスを発揮し、自己回帰項と移動平均項の次数が低い場合は、代替モデルも考慮してください。項の数が少ないモデルは、解釈が容易で、予測能力が向上します。項の数が少ないモデルでは、冗長な項が含まれる可能性も低くなります。たとえば、季節的自己回帰項は、季節移動平均項と重複することがあります。冗長な項は、係数の推定値を不安定にすることがあります。不安定な係数は以下のような結果を生みます。

係数は、予測変数と応答の間に有意な関係が存在する場合でも、有意でなく見える場合があります。
高度に相関する予測変数の係数がサンプル間で大きく異なる。
モデルから高度に相関する項を除外すると、他の高度に相関する項の推定された係数に大きく影響を及ぼします。相関の高い項の係数の符号が誤っている場合もあります。

* 警告 * 定数項を含まない無数の ARIMA(p, d, q) モデル:
(2, 1, 2)

モデル選択

モデル (d = 1)	LogLikelihood	AICc（修正済み赤池情報量基準）	AIC	BIC（ベイズ情報量基準）
p = 0, q = 2*	-197.052	400.878	400.103	404.769
p = 1, q = 2	-196.989	403.311	401.978	408.199
p = 1, q = 0	-201.327	407.029	406.654	409.765
p = 2, q = 0	-200.239	407.251	406.477	411.143
p = 1, q = 1	-200.440	407.655	406.880	411.546
p = 2, q = 1	-201.776	412.884	411.551	417.773
p = 0, q = 1	-204.584	413.542	413.167	416.278
p = 0, q = 0	-213.614	429.350	429.229	430.784

主要な結果AICc、BIC、および AIC

ARIMA(0, 1, 2) の値は AICc です。以下の ARIMA 結果は、ARIMA(0, 1, 2) モデルに対するものです。モデルがデータに十分に適合しない場合は、ARIMA(1, 1, 2) モデルや ARIMA (1, 1, 1) モデルなど、同様のパフォーマンスを持つ他のモデルを検討してください。どのモデルもデータに十分に適合しない場合は、別の種類のモデルを使用するかどうかを検討してください。

ステップ 2: モデル内の各項が有意かどうかを判断する

モデルにおける応答と各項の間の関係が統計的に有意かどうか判断するには、項のp値と有意水準を比較して帰無仮説を評価します。帰無仮説は、項は0と有意に異なっていないというもので、これは、項と応答の間に関連性が存在しないことを意味します。通常、0.05の有意水準（αまたはアルファとも呼ばれる）が有効に機能します。有意水準が0.05の場合は、0と有意に異なっているのに、項が0から有意に異なっていないと結論付けるリスクが5%あることを示します。

p値 ≤ α：項が統計的に有意である: p値が有意水準以下の場合、係数は統計的に有意であると結論付けることができます。
p値 > α：項が統計的に有意ではない: p値が有意水準より大きい場合は、係数は統計的に有意であると結論付けることはできません。項を持たないモデルを再適合したいと考えるかもしれません。

パラメータの最終推定値

タイプ	係数	係数の標準誤差	t値	p値
AR 1	-0.504	0.114	-4.42	0.000
定数	150.415	0.325	463.34	0.000
平均	100.000	0.216

主要な結果: P、コーフ

自己回帰項には、有意水準が0.05未満のp値が入っています。よって、自己回帰項の係数は統計的に有意であると結論付けることができ、モデルにその項を維持する必要があります。

ステップ3：モデルが分析の仮定を満たすかどうか判断する

リュング-ボックスカイ二乗統計量および残差の自己相関関数を使用して、残差は独立しているという仮定をモデルが満たすかどうかを判断します。仮定を満たさない場合、そのモデルはデータに適合しない可能性があり、結果の解釈は慎重に行う必要があります。

リュング-ボックスカイ二乗統計量: 残差が独立しているかどうかを判断するには、p値を各カイ二乗統計量の有意水準と比較します。通常は、有意水準（αまたはアルファとも呼ばれる）として0.05が適切です。p値が有意水準より大きい場合、残差は独立しており、モデルは仮定を満たすと結論付けることができます。
残差の自己相関関数: 有意な相関が存在しない場合は、残差は独立していると結論付けることができます。ただし、季節の遅れではない次数の高い遅れにおいて、1つまたは2つの有意な相関が認められることがあります。これらの相関は、通常、ランダム誤差によって発生するものであり、仮定が満たされないことの証拠ではありません。この場合は、残差は独立していると結論付けることができます。

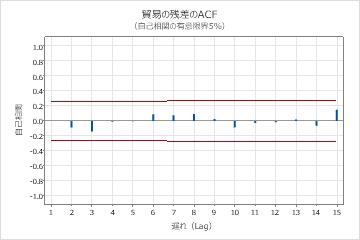
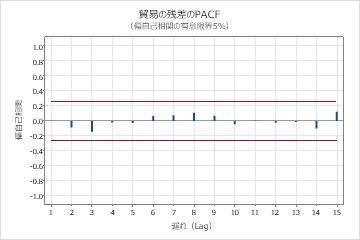
主要な結果：p値、残差のACF
これらの結果において、リュング-ボックスカイ二乗統計量のp値はすべて0.05より大きく、残差の自己相関関数の相関はどれも有意ではありません。よってこのモデルは、残差は独立しているという仮定を満たすと結論付けることができます。

遅れ (Lag)	12	24	36	48
カイ二乗	4.05	12.13	25.62	32.09
自由度	10	22	34	46
p値	0.945	0.955	0.849	0.940