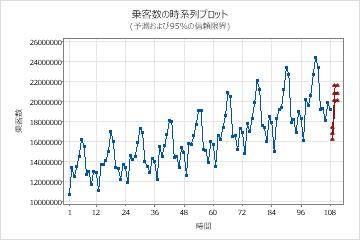
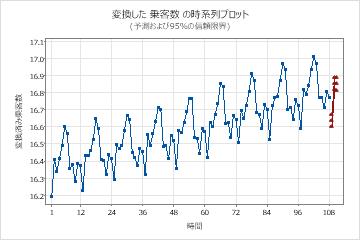
アナリストは、108ヶ月間の航空会社の乗客数に関するデータを収集しました。アナリストは、ARIMA モデルを使用してデータの予測を生成したいと考えています。分析者は以前、データの時系列プロットを調べ、季節サイクルの変動が時間の経過とともに増加することを観察しました。アナリストは、データの自然対数変換が適切であると結論付けました。変換後、分析者は変換されたデータの時系列プロットと変換されたデータの自己相関関数(ACF)プロットを調べました。どちらのプロットも、モデルの開始点が、非季節差分の順序として1を選択し、季節差分の順序に1を選択することであることを示唆しています。アナリストは、今後 3 か月間の予測を要求します。
- サンプルデータ航空旅客.MWXを開きます。
- を選択します。
- 系列に乗客数を入力します。
- で1を選択します差分次数d。
- 期間に 12 を選択して 季節モデルに期間を合わせる 入力します。
- で1を選択します季節差分次数D。
- 予測数に、3と入力します。
- オプションを選択します。
- Box-Cox変換でλ = 0 (自然対数)を選択します。
- 各ダイアログボックスで選択 OK します。
結果を解釈する
モデル選択テーブルは、AICc ごとに検索からモデルをランク付けします。ARIMA(0, 1, 1)(1, 1, 0) モデルの AICc は最小です。以下の ARIMA の結果は、ARIMA(0, 1, 1)(1, 1, 0) モデルに対するものです。
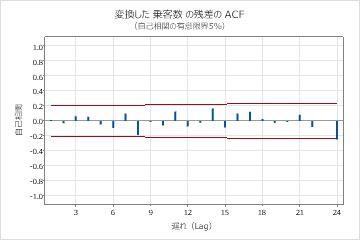
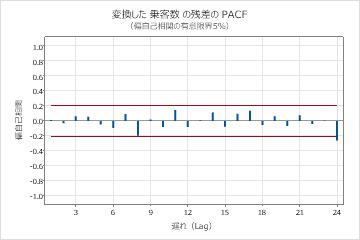
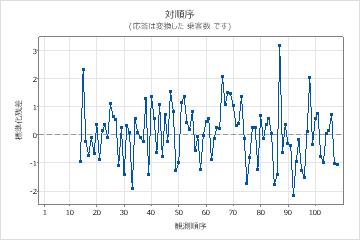
パラメータ表のp値は、モデル項が水準0.05で有意であることを示しています。分析者は、係数がモデルに属していると結論付けます。修正ボックス-ピアス(Ljung-Box)統計量のp値は、水準0.05ではすべて有意ではありません。残差のACFと残差のPACFは、ラグ24でスパイクを示します。通常、ラグ数が大きい場合の大きなスパイクは偽陽性であり、検定統計量はすべて有意ではないため、分析者は、モデルが残差が独立しているという仮定を満たしていると結論付けます。アナリストは、予測の調査は合理的であると結論付けています。
方法
| 季節期間 | 12 |
|---|---|
| 最適なモデルの基準 | 最小 AICc |
| Box-Cox変換 | |
| ユーザー指定の λ | 0 |
| 変換した系列 = ln(乗客数) | |
| 使用中の行 | 108 |
| 未使用の行 | 0 |
モデル選択
| モデル (d = 1, D = 1) | LogLikelihood | AICc(修正済み 赤池情報量基準) | AIC | BIC(ベイズ情 報量基準) |
|---|---|---|---|---|
| p = 0, q = 1, P = 1, Q = 0* | 243.477 | -480.690 | -480.954 | -473.292 |
| p = 2, q = 0, P = 0, Q = 1 | 243.903 | -479.362 | -479.806 | -469.590 |
| p = 1, q = 1, P = 1, Q = 0 | 243.496 | -478.547 | -478.992 | -468.776 |
| p = 0, q = 2, P = 1, Q = 0 | 243.480 | -478.516 | -478.961 | -468.745 |
| p = 2, q = 0, P = 1, Q = 1 | 244.424 | -478.174 | -478.848 | -466.079 |
| p = 0, q = 1, P = 0, Q = 0 | 237.930 | -471.729 | -471.859 | -466.752 |
| p = 1, q = 2, P = 0, Q = 0 | 239.930 | -471.415 | -471.859 | -461.644 |
| p = 1, q = 1, P = 0, Q = 0 | 237.929 | -469.594 | -469.858 | -462.196 |
| p = 0, q = 2, P = 0, Q = 0 | 237.924 | -469.584 | -469.848 | -462.186 |
| p = 1, q = 0, P = 0, Q = 1 | 237.442 | -468.619 | -468.883 | -461.221 |
| p = 1, q = 0, P = 1, Q = 1 | 237.551 | -466.658 | -467.102 | -456.887 |
| p = 2, q = 2, P = 0, Q = 0 | 238.267 | -465.860 | -466.534 | -453.765 |
| p = 2, q = 0, P = 0, Q = 0 | 232.478 | -458.693 | -458.957 | -451.295 |
| p = 0, q = 0, P = 0, Q = 1 | 226.062 | -447.993 | -448.124 | -443.016 |
| p = 0, q = 0, P = 1, Q = 1 | 226.282 | -446.300 | -446.563 | -438.902 |
| p = 2, q = 1, P = 0, Q = 0 | 226.105 | -443.766 | -444.211 | -433.995 |
| p = 1, q = 0, P = 0, Q = 0 | 222.409 | -440.687 | -440.818 | -435.710 |
| p = 2, q = 0, P = 1, Q = 0 | 220.456 | -432.467 | -432.911 | -422.696 |
| p = 0, q = 0, P = 1, Q = 0 | 218.236 | -432.342 | -432.472 | -427.364 |
| p = 1, q = 2, P = 1, Q = 1 | 220.708 | -428.461 | -429.416 | -414.092 |
| p = 0, q = 2, P = 0, Q = 1 | 215.116 | -421.787 | -422.232 | -412.016 |
| p = 0, q = 1, P = 0, Q = 1 | 213.007 | -419.751 | -420.015 | -412.353 |
| p = 2, q = 1, P = 0, Q = 1 | 214.469 | -418.265 | -418.939 | -406.169 |
| p = 1, q = 0, P = 1, Q = 0 | 211.232 | -416.199 | -416.463 | -408.801 |
| p = 2, q = 2, P = 0, Q = 1 | 213.877 | -414.799 | -415.754 | -400.431 |
| p = 2, q = 2, P = 1, Q = 1 | 214.698 | -414.109 | -415.397 | -397.520 |
| p = 1, q = 2, P = 0, Q = 1 | 211.492 | -412.310 | -412.984 | -400.215 |
| p = 1, q = 1, P = 0, Q = 1 | 208.149 | -407.854 | -408.299 | -398.083 |
| p = 0, q = 1, P = 1, Q = 1 | 204.745 | -401.046 | -401.490 | -391.275 |
| p = 0, q = 2, P = 1, Q = 1 | 203.978 | -397.282 | -397.956 | -385.187 |
| p = 1, q = 1, P = 1, Q = 1 | 203.564 | -396.453 | -397.127 | -384.358 |
| p = 1, q = 2, P = 1, Q = 0 | 170.812 | -330.950 | -331.624 | -318.855 |
| p = 2, q = 2, P = 1, Q = 0 | 167.845 | -322.735 | -323.690 | -308.367 |
| p = 2, q = 1, P = 1, Q = 0 | -202.538 | 415.751 | 415.076 | 427.846 |
パラメータの最終推定値
| タイプ | 係数 | 係数の標準誤差 | t値 | p値 |
|---|---|---|---|---|
| SAR (季節変動自己回帰) 12 | -0.403 | 0.103 | -3.92 | 0.000 |
| MA 1 | 0.8704 | 0.0510 | 17.08 | 0.000 |
モデル要約
| 自由度 | 平方和 | 平均平方 | MSD | AICc(修正済み 赤池情報量基準) | AIC | BIC(ベイズ情 報量基準) |
|---|---|---|---|---|---|---|
| 93 | 0.0311326 | 0.0003348 | 0.0003277 | -480.690 | -480.954 | -473.292 |
修正されたBox-Pierce (Ljung-Box) カイ二乗統計量
| 遅れ (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| カイ二乗 | 9.47 | 26.44 | 33.99 | 50.66 |
| 自由度 | 10 | 22 | 34 | 46 |
| p値 | 0.489 | 0.233 | 0.468 | 0.295 |
オリジナル系列
| 95% 限界 | ||||
|---|---|---|---|---|
| 期間 | 予測 | 下限 | 上限 | 実測値 |
| 109 | 16822664 | 16227242 | 17434097 | |
| 110 | 20823876 | 20080751 | 21587153 | |
| 111 | 20826702 | 20077443 | 21596450 | |
変換シリーズ
| 95% 限界 | |||||
|---|---|---|---|---|---|
| 期間 | 予測 | SE 予測 | 下限 | 上限 | 実測値 |
| 109 | 16.6381 | 0.0182964 | 16.6022 | 16.6739 | |
| 110 | 16.8514 | 0.0184495 | 16.8153 | 16.8876 | |
| 111 | 16.8516 | 0.0186014 | 16.8151 | 16.8880 | |