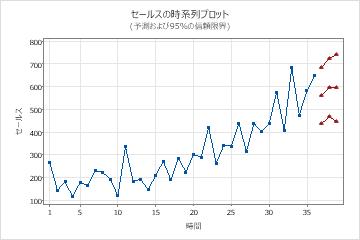
あるマーケティングアナリストは、ARIMAモデルを使用してシャンプー製品の売上の短期予測を生成したいと考えています。アナリストは、過去 3 年間の売上データを収集します。分析者は以前、時系列プロットと系列の自己相関関数(ACF)プロットを調べました。どちらのプロットも、非季節差分の次数の始点として1を示唆しています。データは時系列プロットで季節パターンを示さないため、分析者は非季節モデルから始めることを選択します。アナリストは、今後 3 か月間の予測を要求します。
- サンプルデータシャンプーの販売.MWXを開きます。
- を選択します。
- 系列にセールスを入力します。
- で1を選択します差分次数d。
- の選択を解除しますモデルに定数項を含める。
- 予測数に、3と入力します。
- OKを選択します。
結果を解釈する
モデル選択テーブルは、AICc ごとに検索からモデルをランク付けします。ARIMA (0, 1, 2) モデルの AICc は最小です。以下の ARIMA の結果は、ARIMA (0, 1, 2) モデルに対するものです。
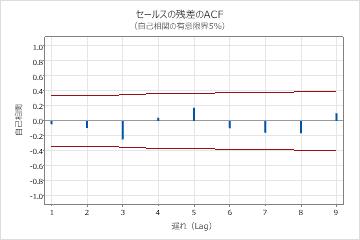
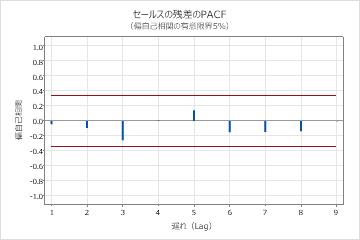
パラメータ表のp値は、移動平均項が0.05水準で有意であることを示しています。分析者は、係数がモデルに属していると結論付けます。修正ボックス-ピアス(Ljung-Box)統計量のp値は、水準0.05ではすべて有意ではありません。残差のACFと残差のPACFはすべて、それぞれのプロットで0.05の制限内にあります。分析者は、モデルが、残差は独立しているという仮定を満たすと結論付けます。アナリストは、予測の調査は合理的であると結論付けています。
方法
| 最適なモデルの基準 | 最小 AICc |
|---|---|
| 使用中の行 | 36 |
| 未使用の行 | 0 |
モデル選択
| モデル (d = 1) | LogLikelihood | AICc(修正済み 赤池情報量基準) | AIC | BIC(ベイズ 情報量基準) |
|---|---|---|---|---|
| p = 0, q = 2* | -197.052 | 400.878 | 400.103 | 404.769 |
| p = 1, q = 2 | -196.989 | 403.311 | 401.978 | 408.199 |
| p = 1, q = 0 | -201.327 | 407.029 | 406.654 | 409.765 |
| p = 2, q = 0 | -200.239 | 407.251 | 406.477 | 411.143 |
| p = 1, q = 1 | -200.440 | 407.655 | 406.880 | 411.546 |
| p = 2, q = 1 | -201.776 | 412.884 | 411.551 | 417.773 |
| p = 0, q = 1 | -204.584 | 413.542 | 413.167 | 416.278 |
| p = 0, q = 0 | -213.614 | 429.350 | 429.229 | 430.784 |
パラメータの最終推定値
| タイプ | 係数 | 係数の標準誤差 | t値 | p値 |
|---|---|---|---|---|
| MA 1 | 1.257 | 0.132 | 9.52 | 0.000 |
| MA 2 | -0.882 | 0.133 | -6.62 | 0.000 |
モデル要約
| 自由度 | 平方和 | 平均平方 | MSD | AICc(修正済み 赤池情報量基準) | AIC | BIC(ベイズ 情報量基準) |
|---|---|---|---|---|---|---|
| 33 | 131017 | 3970.21 | 3743.34 | 400.878 | 400.103 | 404.769 |
修正されたBox-Pierce (Ljung-Box) カイ二乗統計量
| 遅れ (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| カイ二乗 | 15.90 | 27.15 | * | * |
| 自由度 | 10 | 22 | * | * |
| p値 | 0.103 | 0.206 | * | * |
期間 36 からの予測
| 95% 限界 | |||||
|---|---|---|---|---|---|
| 期間 | 予測 | SE 予測 | 下限 | 上限 | 実測値 |
| 37 | 563.193 | 63.0096 | 439.669 | 686.717 | |
| 38 | 594.912 | 65.0499 | 467.388 | 722.435 | |
| 39 | 594.912 | 76.0553 | 445.813 | 744.010 | |