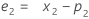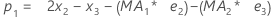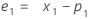Minitab® サポート

二重指数平滑化の方法と計算式

Minitab についての 詳細
目的の方法または計算式を選択します。

このトピックの内容

モデル方程式

二重指数平滑化では、各期間の水準成分とトレンド成分を1つずつ使用します。二重指数平滑化では、2つの重み値（平滑化パラメータとも呼ばれます）を使用して各期間の成分が更新されます。二重指数平滑化の方程式は次のとおりです。

計算式

Lt= αYt+ (1 – α) [Lt–1 + Tt–1]

Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1

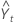= Lt−1 + Tt−1

最初の観測値に番号1を付す場合は、処理を進めるため、時間ゼロでの水準推定値とトレンド推定値を初期化する必要があります。使用する初期化方法により、平滑化値を取得する場合に使用されるのが、Minitabによって生成される最適な重み値なのか、またはユーザーが指定する重み値なのかが決まります。

表記

用語説明
Lt時間tでの水準
α水準の重み値
Tt時間tでのトレンド
γトレンドの重み
Yt時間tでのデータ値
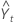時間tの予測値

重み

最適ARIMAの重み

  1. Minitabでは、平方誤差の和を最小化するため、ARIMA (0,2,2)モデルをデータに当てはめます。
  2. その後、トレンド成分と水準水分が後向き予測によって初期化されます。

指定した重み

  1. Minitabでは、線形回帰モデルを、時系列データ（y変数）対時間（x変数）に当てはめます。
  2. この回帰から得られる定数は水準成分の初期推定値であり、傾き係数はトレンド成分の初期推定値です。

等根のARIMA（0,2,）モデルに対応する重みを指定すると、Holtの方法はBrownの方法に合わせて特化されます。1.

水準とトレンドの初期値を計算する方法

統計 > 時系列 > 二重指数平滑化で水準とトレンドの推定値を保存できます。Minitabでは、ダイアログボックスで指定したオプションに応じて、次のいずれかの方法でこれらの列の最初の行の値を計算します。

二重指数平滑化で 最適ARIMAオプションを選択すると、次の方法で水準とトレンドの最初の値が計算されます。これらの手順は、手作業で実行できます。

  1. ARIMA を使用して最適な重み値を計算するように統計 > 時系列 > ARIMA (自己回帰和分移動平均)を選択します。以下のようにダイアログボックスに入力します。
    1. 自己回帰に、0と入力します。
    2. 差分に、2と入力します。
    3. 移動平均に、2と入力します。
    4. モデルに定数項を含めるのチェックを外します。
    5. 保存をクリックし、残差をチェックします。各ダイアログボックスのOKをクリックします。
  2. Minitabでは、ARIMA出力のMA値を使用して、次のように最適な重みを計算します。

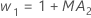
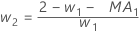
  3. 次に、Minitabは、後の観測値からのデータを使用して、初期観測値に戻って計算します。
    ここで、
    用語説明
    pii番目に平滑化された観測の予測値
    xi時系列でi番目の観測値の値
    ei上記の ARIMA から格納された i番目の残差の値
  4. 水準(L1)の初期値が計算されます。

  5. トレンド(T1)の初期値が計算されます。

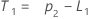
二重指数平滑化ダイアログボックスの平滑化で用いる重みで水準とトレンドに対して独自の重みを指定した場合、Minitabは次の方法を使用して水準とトレンドの初期値を計算します。これらの手順は、手作業で実行できます。
  1. 時系列データの列の長さと等しい時間インデックスの列を作成します。1からnまでの整数の列で十分です。
  2. 統計 > 回帰 > 回帰 > 回帰モデルの適合を選択します。
  3. 応答に、時系列データの列を入力します。連続予測変数で、時間インデックスの列を入力します。
  4. 保存をクリックし、係数をチェックします。各ダイアログボックスのOKをクリックします。
  5. 水準の初期値は次のようになります：

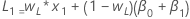
  6. トレンドの初期値は次のようになります：

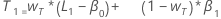    ここで、
    用語説明
    L1水準の初期値
    x1時系列で最初の観測値の値
    T1トレンドの初期値
    wL水準の重み値
    wTトレンドの重み値
    β0回帰モデルの定数項の係数
    β1回帰モデルの予測項の係数

予測

二重指数平滑化では、水準成分とトレンド成分を使用して予測値を生成します。時間tの時点よりm期間先の予測は、次のように計算されます。

計算式

Lt + mTt

予測原点時間までのデータが平滑化に使用されます。

表記

用語説明
Lt時間tでの水準
Tt時間tでのトレンド

予測限界

計算式

平均絶対偏差（MAD）に基づいています。上限と下限の計算式は次のようになります。
  • 上限 = 予測値 + 1.96 × dt × MAD
  • 下限 = 予測値 – 1.96 × dt × MAD

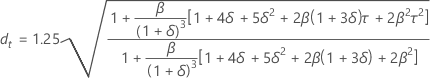
表記

用語説明
β max{α, γ)
δ1 – β
α水準平滑化定数
γトレンド平滑化定数
τ
b0(T)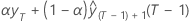
b1(T)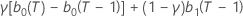

MAPE

平均絶対パーセント誤差（MAPE）により、当てはめられた時系列値の精度を測定します。MAPEでは、精度をパーセントで表します。

計算式

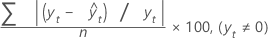
表記

用語説明
yt 時間tでの実際の値
適合値
n 観測値数

MAD

平均絶対偏差（MAD）により、適合された時系列の値の精度を測定します。MADでは、精度がデータと同じ単位で表されるため、誤差の量を概念化するのに役立ちます。

計算式

表記

用語説明
yt 時間tでの実際の値
適合値
n 観測値数

MSD

平方平均偏差（MSD）は、モデルに関係なく、必ず同じ分母nを使用して計算されます。MSDは、MADよりも高感度な、異常に大きな予測誤差の測度です。

計算式

表記

用語説明
yt 時間tでの実際の値
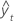適合値
n 観測値数
1 N.R. Farnum and L.W. Stanton (1989). Quantitative Forecasting Methods. PWS-Kent.
Copyright © 2025 Minitab, LLC. All rights Reserved.