このトピックの内容
長さ
時系列に含まれる観測値の数。
欠損値の数
時系列内の欠損値の数。
適合されたトレンド式
適合されたトレンド式を使用して、特定の期間のトレンド成分を計算します。適合されたトレンド式は、トレンド式の代数表現です。適合されたトレンド式の形式は、Yt = b0 + (b1 * t)です。
- ytは変数です
- b0は定数です
- b1は傾きです
- tは時間単位の値です
Minitabでは、適合されたトレンド式と季節指標を使用して、予測値を計算します。
解釈
Minitabでは、適合されたトレンド式を使用してトレンド成分を計算し、季節指標と併用して予測値を計算します。たとえば、次のような適合されたトレンド式があるとします。
Yt = 173.06 + 2.111*t
3番目の期間のトレンド成分は、173.06 + 2.11*3 = 182です。
Minitabでは、データをトレンド成分で除算する(乗法的モデル)か、またはデータからトレンド成分を減算する(加法的モデル)ことにより、トレンド除去データを計算します。
季節指標と季節性
季節指標(元データの表では「季節性」とも呼ばれます)は、時間tにおける季節的な影響です。Minitabでは、データを季節指標によって除算する(乗法的モデル)か、データから季節指標を減算する(加法的モデル)ことにより、データの季節的な影響を調整します。またMinitabでは、適合されたトレンド式と季節指標を使用して、予測値を計算します。
MAPE
平均絶対パーセント誤差(MAPE)では、精度を誤差のパーセント値として表します。MAPEはパーセント値であるため、他の測度統計量よりも容易に理解できます。たとえば、MAPEが5の場合、予測値は平均で5%外れます。
ただし、データに対するモデルの適合度が高いように見える場合でも、MAPEの値が非常に大きくなることがあります。プロットを調べ、いずれかのデータ値が0に近いかどうか確認します。MAPEでは絶対誤差を実際のデータで除算するため、値が0に近いとMAPEの値が非常に大きくなります。
解釈
異なる時系列モデルの適合度を比較するために使用します。値が小さいほど適合性が高いことを示します。単一のモデルに、3つすべての精度の測度の最低値が含まれていない場合、通常はMAPEが優先される測定方法となります。
精度の測度は、1期間先の残差に基づいています。各時点でこのモデルを使用して、時系列における次の期間のY値を予測します。予測値(適合度)と実際のY値の差は、1期間先の残差です。このため、この精度の測度は、データの終わりから始まる1期間を予測する場合に期待される精度を示します。したがって、1期間より先の予測の精度を示すものではありません。予測でモデルを使用する場合は、精度の測度のみに基づいて決定しないでください。モデルの適合度も調べて、特に系列の終わりにおいてその予測とモデルがデータに密接に従うことを確認する必要があります。
MAD
平均絶対偏差(MAD)により、データと同じ単位で精度を表現し、誤差の量を概念化することができます。外れ値の影響は、MSDの場合よりMADの場合のほうが小さくなります。
解釈
異なる時系列モデルの適合度を比較する目的で使用します。値が小さいほど適合性が高いことを示します。
精度の測度は、1期間先の残差に基づいています。このモデルは、各時点において、時系列の次の期間におけるY値を予測する目的で使用します。予測値(適合度)と実際のY値の差は、1期間先の残差です。このため、この精度の測度は、データの終わりから始まる1期間について予測する場合に期待される精度を示します。したがって、1期間より先の予測の精度を示すものではありません。予測でモデルを使用する場合は、精度の測度のみに基づいて決定しないでください。モデルの適合度も調べ、特に系列の終わりに、その予測値とモデルがデータに密接に従うことを確認する必要があります。
MSD
平均平方偏差(MSD)により、当てはめられた時系列の値の精度を測定します。外れ値の影響は、MADの場合よりMSDの場合のほうが大きくなります。
解釈
異なる時系列モデルの適合度を比較する目的で使用します。値が小さいほど適合性が高いことを示します。
精度の測度は、1期間先の残差に基づいています。このモデルは、各時点において、時系列の次の期間におけるY値を予測する目的で使用します。予測値(適合度)と実際のY値の差は、1期間先の残差です。このため、この精度の測度は、データの終わりからの1期間を予測する場合に期待される精度を示します。したがって、1期間より先の予測の精度を示すものではありません。予測でモデルを使用する場合は、精度の測度のみに基づいて決定しないでください。モデルの適合度も調べて、特に系列の終わりにその予測とモデルがデータに密接に従うことを確認する必要があります。
トレンド
トレンド値は、適合されたトレンド式から計算されるトレンド成分です。
解釈
特定の期間のトレンド成分は、データセットの観測値ごとに特定の時間値を、適合されたトレンド式に入力することによって計算されます。たとえば、適合されたトレンド式がYt = 5 + 10 * tの場合、時間2でのトレンド値は25(25 = 5 + 10(2))になります。
トレンド除去
トレンド除去値は、トレンド成分が除去されたデータです。トレンド除去値は、観測値とトレンド値の差(加法的モデル)か、または観測値とトレンド値の間の比率(乗法的モデル)です。
年間化
年間化値は、季節成分が除去されたデータです。年間化値は、観測値と季節値の間の差(加法的モデル)か、または観測値を季節値で除算した値(乗法的モデル)です。
予測
予測値は適合値とも呼ばれます。予測値は、時間(t)における変数の点推定です。
観測値からの差が非常に大きな予測値を含む観測値は、異常な観測値か、または影響力のある観測値である可能性があります。外れ値がある場合は原因の特定を試みてください。データ入力誤差や測定誤差はすべて修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
誤差
誤差値は残差とも呼ばれます。誤差値は、観測値と予測値の差です。
解釈
誤差値をプロットして、モデルが適合するかどうかを判断します。誤差値は、データに対するモデルの適合度を示す有効な情報です。一般に、誤差値は0付近にランダムに分布し、明確なパターンや異常値を示しません。
期間
Minitabには、予測を行う期間が表示されます。期間は、予測の時間単位です。予測は、デフォルトでデータの終わりに開始されます。
予測
予測は、時系列モデルから得られる適合値です。指定した予測数が表示されます。予測は、データの最後または指定した起点から始まります。
解釈
予測を使用して、指定された期間の変数を予測します。たとえば、倉庫管理者は、過去60か月間の発注状況に基づいて、向こう3か月間の製品の発注量をモデル化することができます。
分解では、固定トレンド線と固定季節指標を使用します。トレンドと季節の指標の両方が固定的であるため、分解を使用して予測を行うのはトレンドと季節性が極めて一定な場合のみでなければなりません。特に、時系列の最後にある実際の値と適合値が一致することを検証することが重要です。季節パターンまたはトレンドがデータの最後にある適合値と一致しない場合はWinterの方法を使用します。
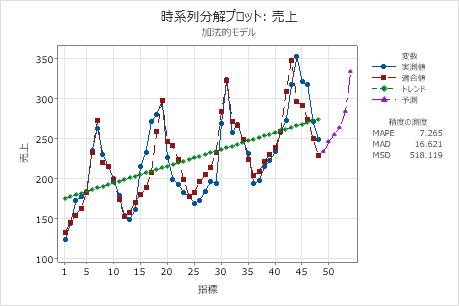
このプロットでは、系列の終わりのデータがモデルによって過小予測されていることが示されています。これは、トレンドまたは季節パターンが一定ではないことを示しています。このデータを予測する場合、Winterの方法を試してデータに対する適合度が高くなるかどうかを判断することができます。
時系列分解プロット
このプロットには、観測値と時間の関係が表示されます。またこのプロットには、トレンド線、トレンド成分と季節成分から計算される適合値、予測値、および精度の測度が含まれます。
解釈

このプロットでは適合値がデータに密接に従っており、これは、そのモデルがデータに適合することを示しています。
成分分析
- 元のデータ
- 元データの時系列プロット
- トレンド除去データ
- トレンド除去値は、トレンド成分が除去されたデータです。トレンド除去値は、観測値とトレンド値の差(加法的モデル)か、または観測値をトレンド値で除算した値(乗法的モデル)です。トレンド除去データのプロットが元データと異なるように見える場合は、データにトレンド成分が存在すると結論付けることができます。
- 季別調整済みデータ
- 季別調整された値は、季節成分が除去されたデータです。季別調整された値は、観測値と季節値の間の差(加法的モデル)か、または観測値を季節値で除算した値(乗法的モデル)です。季別調整済みデータのプロットが元データと異なるように見える場合は、データに季節成分が存在すると結論付けることができます。
- Seas.(季節) Adj.(調整)およびDetr.(トレンド除去) データ
- 季別調整された値とトレンド除去された値は、残差とも呼ばれます。残差は、観測値と予測値の差です。プロットを調べて、モデルが適切かどうか判定します。残差は、0付近にランダムに分布し、明確なパターンや異常値がありません。
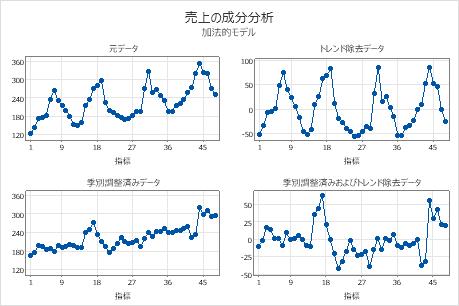
このプロットでは、トレンド除去データと季別調整済みデータが、元の観測値と異なるように見えます。この場合は、データにトレンド成分と季節成分が存在すると結論付けることができます。データの終わり近くにある大きな正の残差は、モデルでそれらの期間が過小予測されていることを示しています。
季節分析
- 季節指標
- 季節指標は、時間tにおける季節の効果です。プロットを使用して、季節効果の方向を決定します。
- 季節によるトレンド除去データ
- トレンド除去データは、トレンド成分が除去されたデータです。箱ひげ図を使用して、最大と最小の変動を示す季節期間を判定します。
- 季節によるパーセントの変動
- プロットには、各季節の変動のパーセントが示されます。このプロットを使用して、各季節期間の変動を数量化します。
- 季節による残差
- 残差は、観測値と予測値の差です。プロットを使用して、残差に季節効果があるかどうかを決定します。
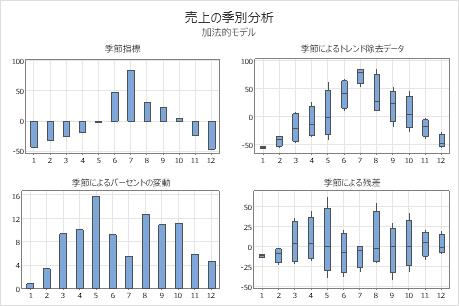
このプロットにおいて、季節指標は、季節の最初の5か月と最後の2か月に平均して下向きの動きがあり、6番目と10番目の月に平均して上向きの動きがあることを示しています。季節によるパーセントの変動の図には、1番目の月の変動が最も小さく、5番目の月の変動が最も大きいことが示されています。季節によるトレンド除去データの箱ひげ図には、季節的な影響の絶対値が大きい月の変動は、季節的な影響が小さい月の変動よりも小さいことが示されています。季節による残差プロットには、残差に対する明確な季節の影響は示されていません。
残差のヒストグラム
残差のヒストグラムには、すべての観測値の残差の分布が表示されます。モデルがデータによく適合する場合は、平均が0のランダム分布になります。したがって、ヒストグラムは、0を中心とするほぼ対称な形になります。
残差の正規確率プロット
残差の正規プロットには、分布が正規分布する場合の残差と期待値の関係が表示されます。
解釈
残差の正規プロットを使用して、残差が正規分布かどうかを判断します。ただし、この分析には、正規分布した残差は不要です。
S曲線は、長い裾を持つ分布を示唆しています。
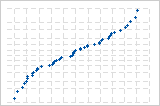
逆S曲線は、短い裾を持つ分布を示唆しています。
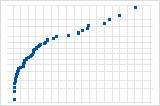
下向きの曲線は、右方向の歪みを示唆しています。
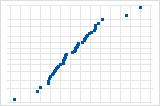
少数の点が直線から離れている場合は、外れ値のある分布を示唆しています。
残差対適合値
残差対適合値プロットでは、y軸に残差が、x軸に適合値が表示されます。
解釈
残差対適合値プロットを使用して、残差に偏りがなく、均一分散かどうかを判断します。理想的なのは、各点が0の両側にランダムにプロットされ、認識可能なパターンが存在しない状態です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
残差に不均一分散またはパターンがある場合、予測は正確ではない可能性があります。
残差対データ順序
残差対データ順序プロットには、データの収集順に残差が表示されます。
解釈
残差対データ順序プロットを使用して、観測期間に観測された値と比較した適合値の正確さを確認します。各点におけるパターンは、モデルがデータに適合しないことを示す可能性があります。理想的には、プロットの残差が中心線の周囲にランダムにプロットされます。
| パターン | パターンが示す意味 |
|---|---|
| 一貫した長期トレンド | モデルはデータに適合しない |
| 短期トレンド | パターンにおけるシフトまたは変化 |
| その他の点から遠い点 | 外れ値 |
| 点での突然のシフト | データの基本的なパターンが変更された |
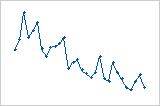
残差は、観測値の順序が左から右に向かって増加するにつれて体系的に減少します。
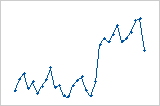
残差の値が低(左)から高(右)に急激に変化しています。
残差対変数
残差対変数プロットには、別の変数に対する残差の値が表示されます。
解釈
このプロットを使用して、変数が系統的に応答に影響するかどうかを判断します。残差にパターンがある場合、その他の変数が応答に関連付けられます。この情報は、追加調査の基本として参考にすることができます。
