相互相関分析を解釈するには、次の手順を実行します。
ステップ1: 自己相関の証拠を探す
2つの系列で自己相関の証拠を探すには、両方の側の相関が0まで漸減する大きな相関の相互相関関数を調べます。通常、自己相関では、2つの時系列間において意味のある関係を見つけるのが困難です。自己相関の証拠が認められる場合は、データを前白色化してください。詳細は、相互相関関数でのデータの前白色化を参照してください。
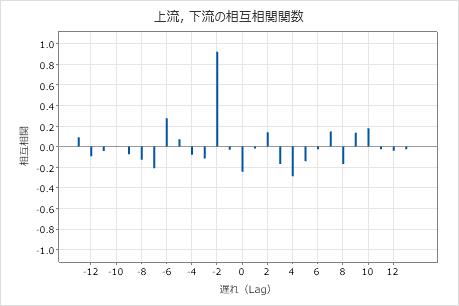
このプロットには、大きな相関があることが示されていますが、両方の側の相関が0まで漸減しません。よってこのプロットは、自己相関の証拠を何も示していません。
ステップ2: 2つの系列の間に関係があるかどうか判断する
2つの系列の間に関係が存在するかどうかを判断するには、両側の相関の中からすぐに有意ではなくなる大きな相関を探します。通常、相関は、絶対値が (nは観測値の数、kは遅れ)よりも大きい場合に有意になります。この計算は、サンプルが大きい正規近似に基づく一般的な手順の規則です。遅れ(Lag)k(k = 1,2 ...)の母集団相互相関がゼロの場合、十分な大きさのnに対し、rxy(k)は、平均(μ)はゼロ、標準偏差(σ)は1/
(nは観測値の数、kは遅れ)よりも大きい場合に有意になります。この計算は、サンプルが大きい正規近似に基づく一般的な手順の規則です。遅れ(Lag)k(k = 1,2 ...)の母集団相互相関がゼロの場合、十分な大きさのnに対し、rxy(k)は、平均(μ)はゼロ、標準偏差(σ)は1/ で近似的に正規分布になります。正規正規母集団のおよそ95%が平均の2つの標準偏差内に存在するため、|rxy(k) |が2/
で近似的に正規分布になります。正規正規母集団のおよそ95%が平均の2つの標準偏差内に存在するため、|rxy(k) |が2/ より大きい場合には遅れkの母集団自己相関がゼロになるという仮説を棄却する検定での有意水準(α)は、およそ5%になります。
より大きい場合には遅れkの母集団自己相関がゼロになるという仮説を棄却する検定での有意水準(α)は、およそ5%になります。

このプロットでは、遅れが-2での相関はおよそ0.92です。0.92 > 0.5547 =  であるため、この相関は有意です。水は、上流の場所から下流の場所に2日間で移動すると結論付けることができます。
であるため、この相関は有意です。水は、上流の場所から下流の場所に2日間で移動すると結論付けることができます。
