アナリストは、108ヶ月間の航空会社の乗客数に関するデータを収集しました。アナリストは、ARIMA モデルを使用してデータの予測を生成したいと考えています。時系列プロットでは、分析者は、高い季節のピークと低い季節のピークの差が時間の経過とともに大きくなることがわかります。このパターンは、分散が定常的ではないことを示しています。分析者はボックスーコックス変換を実行して、分析者がARIMAモデルに適合する前に分散を定常化します。
- サンプルデータ航空旅客.MWXを開きます。
- を選択します。
- 系列にを入力します乗客数。
- 季節期間に、12と入力します。
- Minitab統計ソフトウェアが使用する変換を検索するように選択 最適のλ します。
- タイムスケールのスタンプ列にを入力します日付。
- 変換系列を次の場所に保存するにを入力します変換。OKをクリックします。
結果を解釈する
方法表には、解析の設定と変換の λ の値が表示されます。
これらの結果では、季節期間は 12 で、解析ではデフォルト範囲の -1 と 2 の間の λ 値が検索されます。λ の最適値はおよそ -0.14 です。分析では、値が 0 に丸められ、自然対数変換が使用されます。
方法
| 季節期間 | 12 |
|---|---|
| 間隔から最適な λ を選択する | [-1, 2] |
| 最適のλ | -0.144439 |
| 丸めた最適 λ | 0 |
| 変換した系列 = ln(乗客数) |
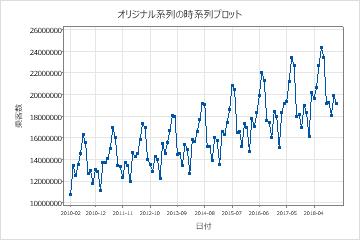
元の系列の時系列を変換された系列の時系列プロットと比較して、変換によって分散が定常になることを確認します。
これらの結果では、元の系列の時系列プロットは非定常分散を示しています。このデータでは、季節サイクルの高値と安値の差は、時間が経つにつれて増加します。このパターンは、時間の経過とともに分散が増加することを示しています。
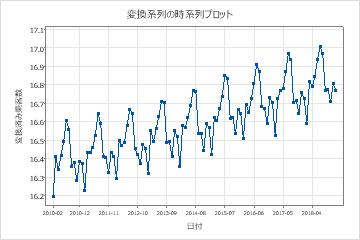
変換された系列の時系列プロットを調べて、変換によって分散が定常になることを確認します。
これらの結果では、変換された系列の時系列プロットは、季節サイクルの高点と安値点の間にほぼ均一な差を示しています。このパターンは、変換によって分散が定常化することを示しています。
また、変換されたデータの時系列プロットを調べて、変換された系列の他の重要な特性を評価します。たとえば、ARIMA モデルの仮定には、系列に定常分散に加えて定常平均があることが含まれます。変換された系列の時系列プロットで、変換された系列に定常平均がないことが示されている場合は、 拡張ディッキーフラーテスト データの差分によって系列の平均が定常的になるかどうかを確認してください。
これらの結果では、変換された系列は上昇傾向を示しています。このパターンは、系列の平均が定常ではないことを示しています。 拡張ディッキーフラーテスト 変換されたデータの格納列で を使用して、差分によって系列が定常的になるかどうかを判断します。