使用する方法または計算式を選択します。
このトピックの内容
ACF
ARIMA残差の自己相関関数(ACF)のグラフには、有意限界を表す線がプロットされます。有意限界を超える値は、およそα = 0.05の場合に統計的に有意であり、自己相関はゼロにならないことの証拠となります。
計算式
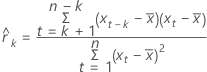
表記
| 用語 | 説明 |
|---|---|
| k | 遅れ; k = 1, 2,... |
| xt | 行tでのxの値 |
 | xの平均 |
| n | 系列内の観測値の数 |
ACFの標準誤差
計算式
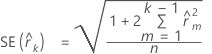
表記
| 用語 | 説明 |
|---|---|
 |  |
| k | 遅れ(Lag); k = 1, 2, ... |
| n | 系列内の観測値の数 |
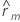 | 遅れmの自己相関 |
t統計量
計算式

表記
| 用語 | 説明 |
|---|---|
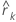 | 遅れkでの自己相関(k = 1, 2, ...) |
 | 遅れkでの自己相関の標準誤差 |
有意限界
計算式
遅れ(Lag)k = tn−1; 0.975 × SE(rk)での上限
遅れ(Lag)k = tn−1; 0.025 × SE(rk)での下限
表記
| 用語 | 説明 |
|---|---|
| SE(rk) | 遅れ(Lag)kでの自己相関の標準誤差 |
| tn-1; 0.975 | 自由度がn - 1のt分布の第97.5百分位数 |
| tn-1; 0.025 | 自由度がn - 1のt分布の第2.5百分位数 |
Ljung-Box Q統計量
計算式
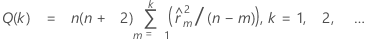
表記
| 用語 | 説明 |
|---|---|
| n | 系列内の観測値の数 |
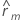 | 遅れm; m = 1, 2, ..., kでの推定自己相関 |
| k | 遅れ(Lag); k = 1, 2, ... |
