このトピックの内容
回帰モデル
| 用語 | 説明 |
|---|---|
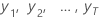 | 時刻の観測時系列値 = 1, ..., T |
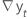 | 時刻 tにおける2つの連続する観測値の差、 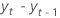 ここで、 t = 2, ..., T ここで、 t = 2, ..., T |
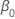 | 回帰モデルにおける定数項 |
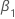 | 回帰モデルにおける線形時間トレンドの係数 |
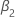 | 回帰モデルにおける 2 次時間トレンドの係数 |
 | 自己回帰プロセスのラグ順序 |
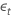 | t = 2, ..., Tの時刻 t における直列独立誤差項 |
- 一定の係数のみを持つモデル

- 一定の係数と線形係数を持つモデル
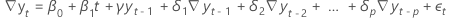
- 定数係数、線形係数、および 2 次係数を持つモデル

- 回帰係数のないモデル
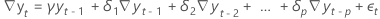
仮説
各拡張ディッキー-フラー検定では、次の仮説を使用します。
帰無仮説H0: 
対立仮説H1: 
帰無仮説は、単位根が時系列サンプル内にあり、データの平均が定常ではないことを意味します。帰無仮説を棄却すると、検定のモデルに応じて、データの平均が定常またはトレンド定常であることを示します。
検定統計量
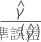
ここで、
| 用語 | 説明 |
|---|---|
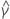 | 最小二乗係数推定値 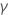 係数 係数 |
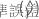 | の最小二乗推定値の標準誤差 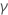 回帰モデルからの係数 回帰モデルからの係数 |
マッキノンの近似p値
帰無仮説では、検定統計量の漸近分布は標準分布に従わない。フラー (1976)1 は、漸近分布の共通百分位数を持つ表を提供します。マッキノン (19942., 2010MacKinnon3)は、応答曲面近似をシミュレーションデータに適用して、ADF検定統計量の任意の値に近似p値を提供します。
分析の仕様で有意水準として0.01、0.05、または0.1を使用する場合、帰無仮説の評価では検定統計量がその有意水準の臨界値と比較されます。検定統計量が臨界値以下の場合は、帰無仮説を棄却します。
分析の仕様で異なる有意水準が与えられた場合、帰無仮説の評価では、近似p値が有意水準と比較されます。p値が有意水準より小さい場合、帰無仮説を棄却します。
有意水準0.01、0.05、および0.1の臨界値
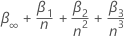
ここで、 n は、回帰モデルを適合するために分析が使用する観測値の数です。の値 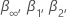 および
および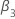 マッキノン(2010)のテーブルから来ています。検定統計量が臨界値以下の場合は、帰無仮説を棄却します。
マッキノン(2010)のテーブルから来ています。検定統計量が臨界値以下の場合は、帰無仮説を棄却します。
近似p値
近似p値の計算はMackinnon (1994)から来ている。p値を有意水準と比較して決定を下します。p値が有意水準以下の場合は、帰無仮説を棄却します。
ラグ順序の決定

ラグ順序の選択は、分析の仕様の基準によって異なります。分析の仕様に基準が含まれていない場合、検定の回帰モデルはpの最大次数 になります。
ラグの順序を決定するための計算では、観測値の数は 、m = n – p – 1になるように最大ラグの順序に依存します。
| 用語 | 説明 |
|---|---|
| n | 観測値の総数 |
| p | モデル内の差分項の最大ラグ順序 |
各基準の計算は次のとおりです。
補正赤池情報量基準(AICc)
分析では、分析の仕様におけるラグ順序ごとに回帰モデルが評価されます。テストのラグ次数は、AIC の最小値を持つ回帰モデルです。

ここで、
| 用語 | 説明 |
|---|---|
| m | 最大ラグ次数に依存する観測値の数 |
| k | モデル内の係数の数 (回帰モデルにゼロ以外の定数がある場合の定数を含む) |
| ティッカー | 回帰モデルの残差平方和 |
ベイズ情報量基準 (BIC)
分析では、分析の仕様におけるラグ順序ごとに回帰モデルが評価されます。テストのラグ次数は、BIC の最小値を持つ回帰モデルです。
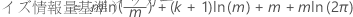
ここで、
| 用語 | 説明 |
|---|---|
| m | 最大ラグ次数に依存する観測値の数 |
| k | モデル内の係数の数 (回帰モデルにゼロ以外の定数がある場合の定数を含む) |
| ティッカー | 回帰モデルの残差平方和 |
t統計量

ここで 、i = 1, ..., p
| 用語 | 説明 |
|---|---|
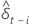 | の最小二乗推定値  回帰モデルの係数 回帰モデルの係数 |
 | の最小二乗推定値の標準誤差  回帰モデルの係数 回帰モデルの係数 |
