ステップ1:データが定常かトレンド定常かを判断する
拡張ディッキー-フラー検定表は、仮説、検定統計量、p値、およびデータを定常的にするために非季節差分を考慮するかどうかに関する推奨事項を提供します。
検定統計量は、帰無仮説を評価する1つの方法を提供します。臨界値以下の検定統計量は、帰無仮説に対する証拠となります。
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
データを差するかどうかを判断するには、検定統計量を臨界値と比較し、p値を有意水準と比較します。p値にはより多くの近似値が含まれているため、分析からの推奨事項では、有意水準が0.01、0.05、または0.10の場合、帰無仮説を評価するために臨界値が使用されます。通常、臨界値とp値の結論は同じです。帰無仮説は、データが非定常であるというものであり、差分がデータを定常化しようとする合理的なステップであることを意味します。
- 有意水準のp値≤
- 検定統計量≤臨界値
- p値が有意水準以下の場合、または検定統計量が臨界値以下の場合、帰無仮説を棄却するという決定が下されます。データはデータが定常的であるという証拠を提供するため、分析の推奨事項は差分なしで続行することです。
- 有意水準>のp値
- 検定統計量>臨界値
- p値が有意水準より大きい場合、または検定統計量が臨界値より大きい場合、帰無仮説を棄却できないという決定になります。データはデータが定常であるという証拠を提供しないため、分析の推奨事項は、差分がデータの平均を定常化するかどうかを判断することです。
データが定常的である場合、検定では差分は推奨されません。差分項を含まない ARIMA モデルを調べます。データが定常でない場合は、差分項を含む ARIMA モデルを調べます。差分データの時系列プロットを使用して、連続する観測値間の差が定常データセットであるかどうかを確認します。差分データが定常的である場合、差分を表す一次項を持つ ARIMA モデルを考慮するのが妥当です。
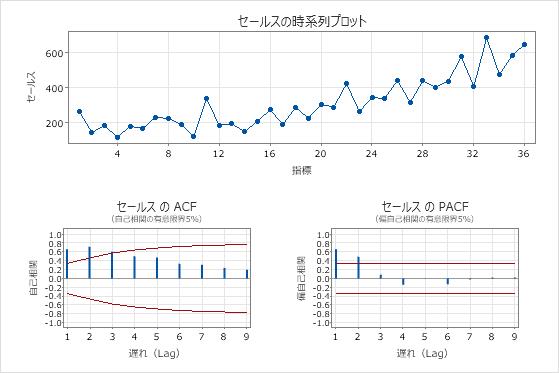
これらの結果では、検定統計量2.29045は臨界値約-2.96053よりも大きくなっています。結果は、データが非定常であるという帰無仮説を棄却できないため、検定の推奨事項は、データを定常的にするために差分を考慮することです。
拡張ディッキーフラーテスト
| 帰無仮説: | データは非定常 |
|---|---|
| 対立仮説: | データは定常 |
| 検定統計量 | p値 | 推奨 |
|---|---|---|
| 2.29045 | 0.999 | テスト統計 > 臨界値 -2.96053 です。 |
| 有意水準 = 0.05 | ||
| 帰無仮説を棄却できません。 | ||
| データを定常化するには、差分化を考慮してください。 |
ステップ2:データの差分による影響を調べる
検定の結論で差分がサポートされている場合は、差分データのプロットを調べて、定常でないデータの特性を調べます。時系列プロットのトレンドは、データの平均が定常ではないことを示すパターンの例です。ACFプロットでは、ゆっくりと減少する大きなスパイクも、データが定常でないことを示します。差分データにこれらのパターンが見られる場合は、ARIMA モデルを 2 次差分で適合させるかどうかを検討します。通常、差分の 1 つまたは 2 つの次数は、データに妥当な適合を提供するのに十分です。
差分データが定常的である場合、合理的なアプローチは、ARIMA モデルに非季節差分の 1 つの順序を含めることです。ARIMA モデルの詳細については、「」を参照してください ARIMA (自己回帰和分移動平均)の概要。
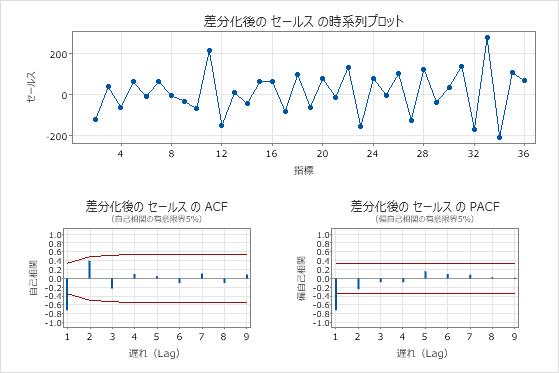
時系列プロットは、差分の結果を示します。これらの結果では、元のデータの時系列プロットは明確な傾向を示しています。差分データの時系列プロットは、連続する値間の差を示します。差分データは、ポイントが変動に明らかなパターンのない水平パスをたどるため、静止しているように見えます。
ACFプロットは、差分の影響も示しています。これらの結果では、元のデータのACFプロットは、ラグ間でゆっくりと減少したスパイクを示しています。このパターンは、データが定常していないことを示します。差分データのACFプロットでは、0と有意に異なる唯一のスパイクはラグ1にあります。
これらの結果では、時系列プロットとACFプロットが検定結果を確認します。したがって、合理的なアプローチは、データの違いをつけてから、自己回帰モデルと移動平均モデルを当てはめて予測を行うことです。