方法の表
方法テーブルには、分析の設定と選択したラグ順序が表示されます。
これらの結果では、分析によって評価される最大ラグ次数は9です。解析では、ラグ次数が 4 が最も高いモデルを使用して、テスト結果を計算します。
方法
| 回帰モデルにおける項の最大ラグオーダー | 9 |
|---|---|
| ラグオーダーの選択基準 | 最小 AIC |
| 追加項 | 定数 |
| 選択したラグオーダー | 4 |
| 使用中の行 | 36 |
拡張ディッキー・フラー・テスト表
拡張ディッキー-フラー検定表は、仮説、検定統計量、p値、および系列を定常化するために差分を考慮するかどうかに関する推奨事項を提供します。
検定統計量は、帰無仮説を評価する1つの方法を提供します。臨界値以下の検定統計量は、帰無仮説に対する証拠となります。
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
データを差するかどうかを判断するには、検定統計量を臨界値と比較し、p値を有意水準と比較します。p値にはより多くの近似値が含まれているため、分析からの推奨事項では、有意水準が0.01、0.05、または0.10の場合、帰無仮説を評価するために臨界値が使用されます。通常、臨界値とp値の結論は同じです。帰無仮説は、データが非定常であるというものであり、差分がデータを定常化しようとする合理的なステップであることを意味します。
- 有意水準のp値≤
- 検定統計量≤臨界値
- p値が有意水準以下の場合、または検定統計量が臨界値以下の場合、帰無仮説を棄却するという決定が下されます。データはデータが定常的であるという証拠を提供するため、分析の推奨事項は差分なしで続行することです。
- 有意水準>のp値
- 検定統計量>臨界値
- p値が有意水準より大きい場合、または検定統計量が臨界値より大きい場合、帰無仮説を棄却できないという決定になります。データはデータが定常であるという証拠を提供しないため、分析の推奨事項は、差分がデータの平均を定常化するかどうかを判断することです。
これらの結果では、検定統計量2.29045は臨界値約-2.96053よりも大きくなっています。結果は、データが非定常であるという帰無仮説を棄却できないため、検定の推奨事項は、データを定常的にするために差分を考慮することです。
拡張ディッキーフラーテスト
| 帰無仮説: | データは非定常 |
|---|---|
| 対立仮説: | データは定常 |
| 検定統計量 | p値 | 推奨 |
|---|---|---|
| 2.29045 | 0.999 | テスト統計 > 臨界値 -2.96053 です。 |
| 有意水準 = 0.05 | ||
| 帰無仮説を棄却できません。 | ||
| データを定常化するには、差分化を考慮してください。 |
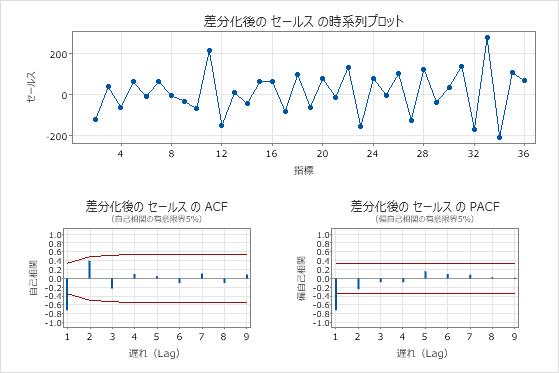
オリジナルシリーズのプロット
- 時系列プロット
- 元の系列の時系列プロットを使用して、元のデータの特性を調べます。トレンドは、非定常平均を示すパターンの例です。差分を使用して、平均を定常化します。
- ACFプロット
- 元のデータから自己相関関数 (ACF) を使用して、データの平均が定常でないことを示すパターンを探します。一般的なパターンは、ラグを横切る大きなスパイクで、非常にゆっくりと消滅します。
- PACFプロット
- 通常、定常データの偏自己相関関数 (PACF) を使用して、ARIMA モデルに自己回帰項が存在することを示すパターンを探します。元のデータが定常でない場合は、差分系列の PACF プロットを使用して、ARIMA モデルの候補項を探します。
これらの結果では、データは時系列プロットで増加傾向を示しています。ACFプロットの最初のラグは、5%の有意限界を超える大きなスパイクを示し、その後非常にゆっくりと減少します。これらのパターンは、データの平均が定常ではないことを示しています。
売上は決定論的傾向を説明する予測変数とは関係がなく、アナリストはARIMAモデルを使用して売上を予測したいと考えているため、データの差分は系列の平均を定常化しようとする合理的な方法です。
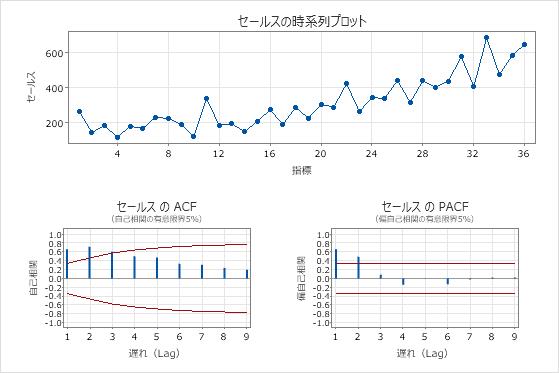
差分系列のプロット
- 差分後の時系列プロット
- 差分データの時系列プロットを使用して、差分によってデータの平均が定常的になることを確認します。時系列プロットは、連続する観測値間の差を示します。定常平均を持つデータは、時系列プロットの水平方向のパスをたどります。
- 差分後のACFプロットとPACFプロット
- 差分データのACFを使用して、差分によってデータの平均が定常になることを確認します。スパイクが急速に減少するプロットは、定常データの特徴です。
これらの結果では、時系列プロットは、差分データの平均と分散がほぼ一定であることを示しています。データは静止しているように見えます。
差分データのACFプロットでは、0と有意に異なる唯一のスパイクはラグ1にあります。このパターンは、データが静止していることも示唆しています。