ARIMA分析を解釈するには、次の手順を実行します。主要な出力には、p値、係数、平均平方誤差、Ljung-Boxカイ二乗統計量、および残差の自己相関関数などがあります。
ステップ1: モデルの各項が有意かどうか判断する
モデルにおける応答と各項の間の関係が統計的に有意かどうか判断するには、項と有意水準を比較して帰無仮説を評価します。帰無仮説は、項は0と有意に異なっていないというもので、これは、項と応答の間に関連性が存在しないことを意味します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準が0.05の場合は、0と有意に異なっているのに、項が0から有意に異なっていないと結論付けるリスクが5%あることを示します。
- p値 ≤ α: 項は統計的に有意です
- p値が有意水準以下の場合、係数は統計的に有意であると結論付けることができます。
- p値 > α: 項は統計的に有意ではありません
- p値が有意水準より大きい場合、係数は統計的に有意であると結論付けることはできません。その項なしでモデルを再び当てはめることができます。
パラメータの最終推定値
| タイプ | 係数 | 係数の標準誤差 | t値 | p値 |
|---|---|---|---|---|
| AR 1 | -0.504 | 0.114 | -4.42 | 0.000 |
| 定数 | 150.415 | 0.325 | 463.34 | 0.000 |
| 平均 | 100.000 | 0.216 |
主要な結果: P、係数
自己回帰項には、有意水準が0.05未満のp値が入っています。よって、自己回帰項の係数は統計的に有意であると結論付けることができ、モデルにその項を維持する必要があります。
ステップ2:データに対するモデルの適合度を判断する
平均平方誤差(MS)を使用して、データに対するモデルの適合度を判断します。値が小さいほど、適合性が高いモデルであることを示します。
残差の平方和
| 自由度 | 平方和 | 平均平方 |
|---|---|---|
| 58 | 366.733 | 6.32299 |
主要な結果:平均平方誤差
このモデルの平均平方誤差は6.323です。この値自体にそれほどの意味はありませんが、この値を使用して異なるARIMAモデルの適合値を比較することができます。
ステップ3:モデルが分析の仮定を満たすかどうか判断する
リュング-ボックスカイ二乗統計量および残差の自己相関関数を使用して、残差は独立しているという仮定をモデルが満たすかどうかを判断します。仮定を満たさない場合、そのモデルはデータに適合しない可能性があり、結果の解釈は慎重に行う必要があります。
- リュング-ボックスカイ二乗統計量
- 残差が独立しているかどうかを判断するには、p値を各カイ二乗統計量の有意水準と比較します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。p値が有意水準より大きい場合、残差は独立しており、モデルは仮定を満たすと結論付けることができます。
- 残差の自己相関関数
- 有意な相関が存在しない場合は、残差は独立していると結論付けることができます。ただし、季節の遅れではない次数の高い遅れにおいて、1つまたは2つの有意な相関が認められることがあります。これらの相関は、通常、ランダム誤差によって発生するものであり、仮定が満たされないことの証拠ではありません。この場合は、残差は独立していると結論付けることができます。
修正されたBox-Pierce (Ljung-Box) カイ二乗統計量
| 遅れ (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| カイ二乗 | 4.05 | 12.13 | 25.62 | 32.09 |
| 自由度 | 10 | 22 | 34 | 46 |
| p値 | 0.945 | 0.955 | 0.849 | 0.940 |
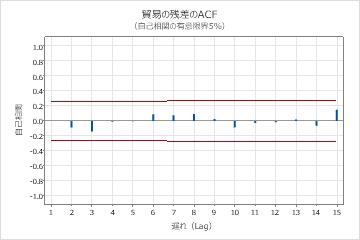
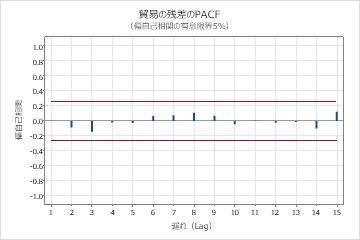
主要な結果:p値、残差のACF
これらの結果において、リュング-ボックスカイ二乗統計量のp値はすべて0.05より大きく、残差の自己相関関数の相関はどれも有意ではありません。よってこのモデルは、残差は独立しているという仮定を満たすと結論付けることができます。
