時系列プロット
時系列プロットには、データが時系列順に表示されます。予測を行うと、予測値とその95%信頼限界がプロットに表示されます。
解釈
- データに異なる変動が存在するかどうかを判断します。異なる変動が存在する場合は、データを変換して変動が一定になるようにする必要があります。
- データが一定平均の周囲に集中しているかどうかを判断します。平均が一定していない場合は、データの階差を取って平均を一定にする必要があります。
残差のACF
プロットには、残差の自己相関関数が示されます。自己相関関数は、k時間単位離れた時系列の観測値間の相関(ytとyt-k)を表す測度です。
解釈
残差の自己相関関数を使用して、残差は独立しているという仮定をモデルが満たすかどうかを判断します。その仮定を満たさない場合、そのモデルはデータに適合しない可能性があり、結果の解釈は慎重に行う必要があります。有意な相関が存在しない場合は、残差は独立していると結論付けることができます。ただし、季節の遅れではない次数の高い遅れにおいて、1つまたは2つの有意な相関が認められることがあります。これらの遅れは、通常、ランダム誤差によるものであり、仮定が満たされていないことの証拠ではありません。したがって、この場合は、残差は独立していると結論付けることもできます。
残差のPACF
偏自己相関関数は、遅れが短いその他のすべての項(yt-1、yt-2、...、yt-k-1)の存在を考慮して調整した後に計算される、k時間単位離れた時系列の観測値間の相関(ytとyt-k)を表す測度です。
解釈
残差の偏自己相関関数を使用して、残差は独立しているという仮定をモデルが満たすかどうかを判断します。その仮定を満たさない場合、そのモデルはデータに適合しない可能性があり、結果の解釈は慎重に行う必要があります。有意な相関が存在しない場合は、残差は独立していると結論付けることができます。
残差のヒストグラム
残差のヒストグラムには、すべての観測値の残差の分布が表示されます。モデルがデータによく適合する場合は、平均が0のランダム分布になります。したがって、ヒストグラムは、0を中心とするほぼ対称な形になります。
残差の正規確率プロット
残差の正規プロットには、分布が正規分布する場合の残差と期待値の関係が表示されます。
解釈
残差の正規プロットを使用して、残差が正規分布かどうかを判断します。ただし、この分析には、正規分布した残差は不要です。
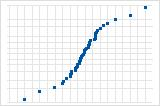
S曲線は、長い裾を持つ分布を示唆しています。
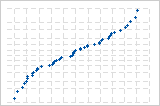
逆S曲線は、短い裾を持つ分布を示唆しています。
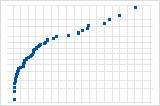
下向きの曲線は、右方向の歪みを示唆しています。
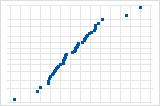
少数の点が直線から離れている場合は、外れ値のある分布を示唆しています。
残差対適合値
残差対適合値プロットでは、y軸に残差が、x軸に適合値が表示されます。
解釈
残差対適合値プロットを使用して、残差に偏りがなく、均一分散かどうかを判断します。理想的なのは、各点が0の両側にランダムにプロットされ、認識可能なパターンが存在しない状態です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
残差に不均一分散またはパターンがある場合、予測は正確ではない可能性があります。
残差対データ順序
残差対データ順序プロットには、データの収集順に残差が表示されます。
解釈
残差対データ順序プロットを使用して、観測期間に観測された値と比較した適合値の正確さを確認します。各点におけるパターンは、モデルがデータに適合しないことを示す可能性があります。理想的には、プロットの残差が中心線の周囲にランダムにプロットされます。
| パターン | パターンが示す意味 |
|---|---|
| 一貫した長期トレンド | モデルはデータに適合しない |
| 短期トレンド | パターンにおけるシフトまたは変化 |
| その他の点から遠い点 | 外れ値 |
| 点での突然のシフト | データの基本的なパターンが変更された |
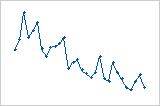
残差は、観測値の順序が左から右に向かって増加するにつれて体系的に減少します。
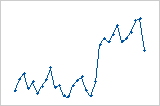
残差の値が低(左)から高(右)に急激に変化しています。
残差対変数
残差対変数プロットには、別の変数に対する残差の値が表示されます。
解釈
このプロットを使用して、変数が系統的に応答に影響するかどうかを判断します。残差にパターンがある場合、その他の変数が応答に関連付けられます。この情報は、追加調査の基本として参考にすることができます。
