ある雇用アナリストは雇用局のために、5年間(60ヶ月)にわたる3つの産業での雇用動向を調査します。分析者がARIMAを実行して小売/卸売業にモデルを当てはめるとします。
- 雇用動向.MWXサンプルデータを開きます。
- を選択します。
- 系列に貿易を入力します。
- 非季別の自己回帰に、「1」と入力します。
- グラフをクリックして、残差のACFを選択します。
- OKをクリックします。
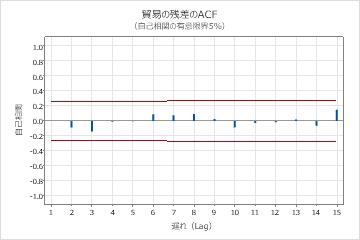
結果を解釈する
自己回帰項には、有意水準が0.05未満のp値が入っています。分析者は、自己回帰項の係数が統計的に0から有意に異なると結論付け、モデルにその項を維持します。Ljung-Boxカイ二乗統計量のp値はすべて0.05より大きく、残差の自己相関関数の相関はどれも有意ではありません。分析者は、モデルが、残差は独立しているという仮定を満たすと結論付けます。
各反復の推定値
| 反復 | 残差平方和 (SSE) | パラメータ | |
|---|---|---|---|
| 0 | 543.908 | 0.100 | 90.090 |
| 1 | 467.180 | -0.050 | 105.068 |
| 2 | 412.206 | -0.200 | 120.046 |
| 3 | 378.980 | -0.350 | 135.024 |
| 4 | 367.545 | -0.494 | 149.372 |
| 5 | 367.492 | -0.503 | 150.341 |
| 6 | 367.492 | -0.504 | 150.410 |
| 7 | 367.492 | -0.504 | 150.415 |
パラメータの最終推定値
| タイプ | 係数 | 係数の標準誤差 | t値 | p値 |
|---|---|---|---|---|
| AR 1 | -0.504 | 0.114 | -4.42 | 0.000 |
| 定数 | 150.415 | 0.325 | 463.34 | 0.000 |
| 平均 | 100.000 | 0.216 |
観測数: 60
残差の平方和
| 自由度 | 平方和 | 平均平方 |
|---|---|---|
| 58 | 366.733 | 6.32299 |
修正されたBox-Pierce (Ljung-Box) カイ二乗統計量
| 遅れ (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| カイ二乗 | 4.05 | 12.13 | 25.62 | 32.09 |
| 自由度 | 10 | 22 | 34 | 46 |
| p値 | 0.945 | 0.955 | 0.849 | 0.940 |

