信頼性データをモデル化するためのワイブル分布の使用
- バーンイン期間中に何パーセントのアイテムが故障すると予測されるでしょうか。たとえば、何パーセントのヒューズが8時間のバーンイン期間中に故障すると予測されるでしょうか。
- 耐用期間内に何件の保証請求が予測されるでしょうか。たとえば、このタイヤの50,000マイルの耐用期間中に何件の保証請求が予測されるでしょうか。
- いつ急速摩耗が起きると予測されるでしょうか。たとえば、エンジンが摩耗段階に入るのを防ぐために定期保守はいつ行う必要があるでしょうか。
ワイブル分布は、右方向に歪んだデータ、左方向に歪んだデータ、対称のデータをモデル化できます。したがって、この分布は、真空管、コンデンサ、ボールベアリング、リレー、材料強度など幅広い応用分野の信頼性を評価するために使用されます。また、ワイブル分布は、減少、増加、または安定するハザード関数をモデル化することも可能で、アイテムの寿命のあらゆる段階を表せます。
ワイブル分布は、化学反応が原因の製品故障や、半導体故障で起こる腐食などの劣化過程が原因の製品故障に対して効果的に機能しない場合があります。一般的にこれらの場合は対数正規分布を使用してモデル化されます。
- Rayleigh分布
- 形状パラメータが2のワイブル分布はRayleigh分布として知られています。この分布は通信工学の分野で、入力屈折損失、変調側波帯注入、搬送波抑圧、RF減衰の測定などの測定データを表すためによく使用されます。また、この分布は電子真空装置の寿命試験にもよく使用されます。
- 最弱リンクモデル
- ワイブル分布は、多くの同一の独立した工程で最初に危機的段階に達した工程によって全体の故障時間が決まる場合の寿命分布をモデル化することもできます。極値理論を基礎とするこの「最弱リンク」モデルでは、多くの欠陥が進行し、最終的にいずれかが故障個所になります。ワイブル分布は最小極値分布から理論的に導くことができるため、コンデンサ、ボールベアリング、リレー、材料強度の故障などの最弱リンク応用分野も効果的にモデル化できます。ただし、ワイブル分布は下限が0で、モデル化できるのは正の値のみであるため、対象の変数が負の値を取り得る場合は最小極値分布の方が適しています。
例1: コンデンサ
コンデンサを高ストレスで試験し、故障データ(時間)を取得しました。故障データはワイブル分布によってモデル化されました。
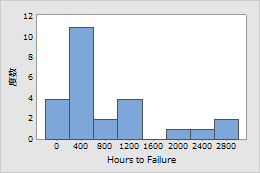
例2: フィラメント
電球の製造会社が、長期間の通常使用で摩耗しないとされる白熱フィラメントを製造しています。この会社のエンジニアは電球を10年間保証したいと考えています。エンジニアは、長期の使用をシミュレートするため電球にストレスをかけ、各電球の故障までの時間数を記録します。
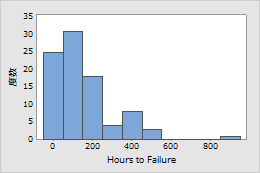
ワイブル分布のパラメータ、信頼性関数、ハザード関数の間の関係
ワイブル分布の形状パラメータβを調整することにより、さまざまな寿命分布の特性をモデル化できます。
0 < ß < 1
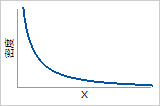
確率密度関数
無限大から指数関数的に減少します
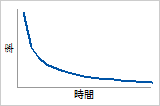
ハザード関数
故障率が最初に高く、時間の経過とともに減少します(「バスタブ」型ハザード関数の最初の部分)
ß = 1
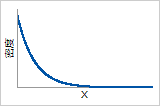
確率密度関数
1/αから指数関数的に減少します(α=尺度パラメータ)

ハザード関数
製品の使用期間中、故障率が一定です(「バスタブ」型ハザード関数の2番目の部分)
ß = 1.5
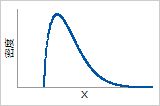
確率密度関数
ピークまで増加し、その後減少します
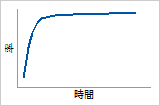
ハザード関数
故障率は最初に大きく増加し、その後も増加し続けます
ß = 2
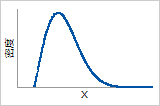
確率密度関数
Rayleigh分布
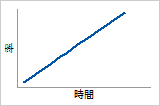
ハザード関数
故障率が線形的に増加します
3 ≤ ß ≤4
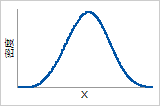
確率密度関数
つりがね型
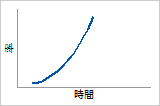
ハザード関数
急速に増加します
ß > 10
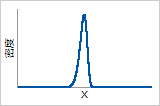
確率密度関数
極値分布に似ています
ハザード関数
非常に急速に増加します
