信頼性データをモデル化するための最小極値分布の使用
最小極値分布は、同じ任意分布から得られるランダム観測値の非常に大きな集合を最小とする限界分布です。この分布は、故障につながる多くの同一の独立した工程のうち最初に故障した工程によって全体の故障時間が決まる場合のモデルとして有効です。これは最悪リンクまたは最弱リンクと呼ばれることもあります。
- 最大の負荷に耐えられるのはどの材料でしょうか。
- 保証期間中に何個の品目が故障すると予測されるでしょうか。
- 袋の各部分のさまざまな位置で複数の強度試験を行う場合、袋を破るのに必要な最小の力はどれだけでしょうか。
- 1,000ポンドの荷重をもっともよく保持するのはどのケーブルでしょうか。
多くの場合、最小極値分布は、負荷や強度に関する製品の故障に適しています。極値分布を使用して最小値をモデル化します。この分布を使用する場合、通常は母集団の大部分を表す変数の分布については考慮せず、故障につながる可能性のある極値についてのみ考慮します。つまり、特定の材料において負荷がかかったときに不均一なストレスの原因となり得る欠陥を調査します。したがって材料の強度は、強度をもっとも大幅に低下させる欠陥(最弱リンク)の影響に関連しています。
最小極値分布とワイブル分布の関係は、正規分布と対数正規分布の関係に似ています。具体的には、ワイブル分布に従う変数のeを底とする対数は最小極値分布に従います。
このような同等性があるにもかかわらず、これらの分布は厳密には置き換えて適用することはできません。アメリカ国立標準技術研究所(NIST、National Institute of Standards and Technology)は、最小極値分布を「目的の変数が、正または負の値を取り得る多くの変量因子の中の最小値である場合のモデル化用途」に使用することを推奨しています。
一般的な用途の1つは、コンデンサの絶縁破壊があります。絶縁破壊では、多くの欠陥のいずれかが最終的に全体の故障の原因となります。別の例は半導体のワイヤボンドです。ワイヤボンドは、極度の電気負荷がかかったりボンド強度が極端に低くない限り、通常の動作環境では破壊や過熱が起こることはありません。同様に、冷却液の管は、熱が冷却液に移りやすいように最小限の厚さになっていますが、管のどこかに燃焼ガスが小さな穴を開けると故障が発生します。
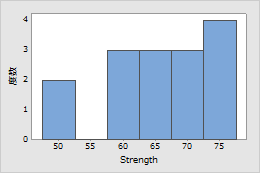
例1: ワイヤ強度
同じ長さのワイヤサンプルの破壊強度を試験しました。結果は最小極値分布を使用してモデル化されています。
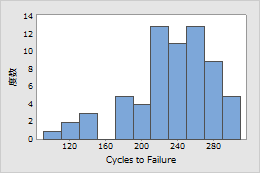
例2: 故障までのサイクル
エンジニアが、合金試料を合計300,000サイクルにかけ、故障までのサイクル数を測定します。
極値分布の確率密度関数とハザード関数
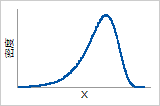
確率密度関数
極値分布では、通常、確率密度関数は左方向に歪みます。
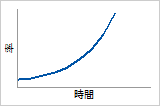
ハザード関数
最小極値分布のハザード関数は、指数関数的に増加する故障リスクを示します。
