信頼性データをモデル化するための対数正規分布の使用
対数正規分布は柔軟な分布で、正規分布と密接に関係しています。この分布は特に、およそ対称または右方向に歪んだデータのモデリングに有効です。ワイブル分布と同様に、対数正規分布は、尺度パラメータによって外見が著しく異なる場合があります。
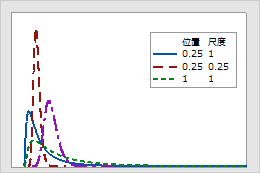
実際、対数正規モデルおよびワイブルモデルは、特定の寿命試験データセットに同様によく適合することがあります。ただし、考慮すべき重要な違いがあります。これらの分布を使用してサンプルデータを超えて外挿する場合、対数正規はワイブル分布よりも早い時間により低い平均故障率を予測します。
対数正規分布は、多くの先端技術応用分野で、最も一般的に使用される寿命分布モデルです。この分布は、乗法成長モデルに基づいています。つまり、任意の瞬間に、工程には現在の状態に比例する劣化のランダムな増加が発生します。これらのランダムな独立した成長すべての乗法効果が累積して故障の原因となります。したがって、この分布は、次の応用分野のような、主にストレスや疲労によって故障する部品のモデル化によく使用されます。
- 半導体故障に一般的な化学反応や、腐食、移動、拡散などの劣化による故障
- 疲労亀裂の成長が発生する金属の破壊までの時間
- 一定の時間後に故障のリスクが減少する電子部品
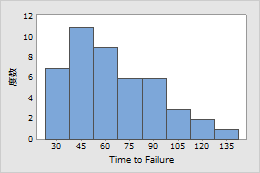
例1: 電子部品
エンジニアは通常の動作条件で電子部品が故障するまでの時間を記録します。部品は時間の経過とともに故障リスクが減少しており、対数正規分布を使用してモデル化できる可能性があります。
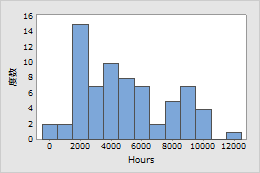
例2: ディーゼル発電機ファン
ディーゼル発動機ファンの使用期間中、故障までの時間を追跡しました。対数正規分布を使用してデータをモデル化しました。
対数正規分布の確率密度関数とハザード関数
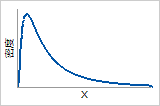
確率密度関数
このデータは右方向に歪んでいます。
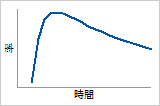
ハザード関数
故障リスクは最大値まで急速に増加してから減少します。
