信頼性データをモデル化するための指数分布の使用
指数分布は、パラメータが1つだけの単純な分布で、信頼性データをモデル化するために一般に使用されています。指数分布は実際にはワイブル分布のß = 1の特殊なケースです。
指数分布は、製品や品目の寿命のうち、新品であるか1年または数年前のものであるかにかかわらず、いつでも故障する可能性が同じという段階をモデル化するのに適しています。つまり、予測される試用期間中で老朽化により損耗が始まる前の段階です。
- 指数分布は、使用されている製品の予測寿命のずっと先まで損耗しないことが一般的な電子部品をモデル化するためによく使用されます。例として、ダイオード、トランジスタ、抵抗器、コンデンサなど、高品質集積回路の部品が挙げられます。
- また、指数分布はバスタブ型曲線の中間部分の特徴である長く「平ら」(比較的一定している)に故障リスクが低い期間をモデル化するのに優れているとされています。この期間は製品の耐用期間に対応し、曲線の「真性故障」部分として知られています。
- ただし、指数分布は、ボールベアリングや特定のレーザーまたはフィラメントなど、製品の予測寿命が終了する前に疲労、腐食、摩耗が予想される機械部品や電子部品のモデル化には使用できません。
指数分布の重要な特性は無記憶性であるということです。無記憶性とは、成分の残りの寿命が現在の年齢に左右されないことを意味します。たとえば、損耗したり破損したりするシステムは、寿命の後の方に障害を起こす可能性が高いため無記憶性ではありません。したがって、この分布は、製品の使用期間全体を通じて故障率が一定である場合に使用します。ユニット当たりの時間内の故障数は、通常、単位時間当たりの故障パーセント(たとえば、1000時間あたりの故障パーセント)で表されます。
例1: トランジスタ
ある電子部品は、製品の予測寿命の間、故障率が一定であることが知られています。エンジニアは通常の動作条件で部品が故障するまでの時間を記録します。
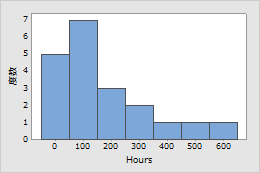
例2: フィラメント
電球の製造会社が、長期間の通常使用で摩耗しないとされる白熱フィラメントを製造しています。この会社では電球を10年間保証したいと考えています。エンジニアは、長期の使用をシミュレートするため電球にストレスをかけ、各電球の故障までの月数を記録します。
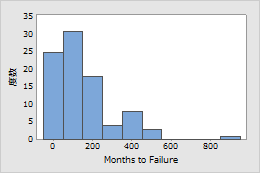
指数分布の確率密度関数とハザード関数
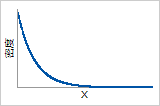
確率密度関数
確率密度関数は、故障データが右方向に歪んでいることを示しています

ハザード関数
ハザード関数は、故障リスクが一定であることを示しています
